MegEngine 快速上手

备注

• 本教程假设读者具有最基础的 Python 代码编程经验，以及了解 “深度学习” 基本概念；

• 在进行下面的步骤之前，请确认你已经按照 如何安装 MegEngine 页面的指示安装好 MegEngine.

  >>> import megengine
  >>> print(megengine.__version__)
  

参见

• 本教程展示模型开发基本流程，对应源码： examples/quick-start.py

• 只关注模型部署流程的用户可以阅读 MegEngine 模型推理部署教程 🚀🚀🚀

概览

这份快速上手教程将引导你：1. 使用 MegEngine 框架开发出经典的 LeNet 神经网络模型； 2. 使用它在 MNIST 手写数字数据集上完成训练和测试；3. 将模型用于实际的手写数字分类任务。

在最开始，我们会对 MNIST 数据集有一个最基本的了解，并尝试使用 MegEngine 中的 data 模块完成 MNIST 数据集的获取和预处理，将其划分成训练数据集和测试数据集； 同时你还会准备好相应的 DataLoader, 负责在后续训练和测试模型时完成数据供给。 紧接着你会用 functional 和 module 模块设计好 LeNet 模型结构。 接下来的步骤也很简单，对模型进行训练！训练的过程中我们需要用到 autodiff 模块和 optimizer 模块，前者在训练的过程中会记录梯度信息， 后者负责根据梯度信息对模型中的参数进行更新，以达到优化的目的。 最终，我们会对训练好的模型进行测试，你也可以用自己的手写数字样本来试试效果~

注意：本教程的目的是为 MegEngine 初见用户展示框架最基本的使用流程， 因此不会对每个步骤以及背后的原理进行非常详细的解释，也不会展现出 MegEngine 的全部特性。 如果你对整个深度学习的流程不是很清楚，不用担心，可以尝试跑通这个教程，最后会有进一步的指引。

数据加载和预处理

数据集介绍

MNIST [1] 手写数字数据集中包含 60,000 张训练图像和 10,000 张测试图像，每张图片是 28x28 像素的灰度图。 如今 MNIST 已然成为机器学习领域的 “Hello, world!”, 用来验证框架和库的可用性。

By Josef Steppan - Own work , CC BY-SA 4.0

获取 MNIST 数据集

在 MegEngine 中可以 使用已经实现的数据集接口 来获取 MNIST 数据集：

from megengine.data.dataset import MNIST

from os.path import expanduser
MNIST_DATA_PATH = expanduser("~/data/datasets/MNIST")

train_dataset = MNIST(MNIST_DATA_PATH, train=True)
test_dataset = MNIST(MNIST_DATA_PATH, train=False)

使用 MegEngine 下载 MNIST 数据集速度慢或总是失败

调用 MegEngine 中的 MNIST 接口将从 MNIST 官网下载数据集，MegEngine 不提供镜像或加速服务。 本质上可以看作是运行了一份单独的 MNIST 数据集获取与处理脚本（你也可以自己编写脚本来搞定这件事）。

在 MegStudio 平台中提供了 MNIST 数据集镜像，需注意：

• 在创建项目时选择 MNIST 数据集，将 MNIST_DATA_PATH 设置为 /home/megstudio/dataset/MNIST/;

• 在调用 MNIST 接口时将 download 参数设置为 False, 避免再次下载。

准备 DataLoader

我们将上一步得到的训练集和测试集作为参数输入给 DataLoader:

import megengine.data as data
import megengine.data.transform as T

train_sampler = data.RandomSampler(train_dataset, batch_size=64)
test_sampler = data.SequentialSampler(test_dataset, batch_size=4)

transform = T.Compose([
    T.Normalize(0.1307*255, 0.3081*255),
    T.Pad(2),
    T.ToMode("CHW"),
])

train_dataloader = data.DataLoader(train_dataset, train_sampler, transform)
test_dataloader = data.DataLoader(test_dataset, test_sampler, transform)

在上面的代码中，我们对数据集的抽样规则和预处理策略也进行了定义， 例如指定了训练集的 batch_size 为 64, 抽样方式为随机抽样… 并分别将对应的 sampler 和 transform 作为构造 DataLoader 的初始化参数提供。

参见

想要了解更多细节，可以参考 使用 Data 构建输入 Pipeline 。

定义模型结构

LeNet [2] 网络模型的结构如下图所示（图片截取自论文）：

Architecture of LeNet a Convolutional Neural Network here for digits recognition. Each plane is a feature map ie a set of units whose weights are constrained to be identical.

在 MegEngine 中定义网络最常见的方式是创建一个继承自 Module 的类：

import megengine.functional as F
import megengine.module as M

class LeNet(M.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = M.Conv2d(1, 6, 5)
        self.conv2 = M.Conv2d(6, 16, 5)
        self.fc1 = M.Linear(16 * 5 * 5, 120)
        self.fc2 = M.Linear(120, 84)
        self.classifier = M.Linear(84, 10)

        self.relu = M.ReLU()
        self.pool = M.MaxPool2d(2, 2)

    def forward(self, x):
        x = self.pool(self.relu(self.conv1(x)))
        x = self.pool(self.relu(self.conv2(x)))
        x = F.flatten(x, 1)
        x = self.relu(self.fc1(x))
        x = self.relu(self.fc2(x))
        x = self.classifier(x)
        return x


model = LeNet()

• 需要在 __init__ 方法中调用 super().__init__;

• 需要在 __init__ 方法中定义需要用到的结构，并在 forward 中定义前向计算过程。

参见

想要了解更多细节，可以参考 使用 Module 定义模型结构 。

训练：优化模型参数

得到前向计算输出后，为了优化模型参数，我们还需要：

• 使用 GradManager 对参数梯度进行管理；

• 使用 Optimizer 进行反向传播和参数更新（以 SGD 为例）。

import megengine.optimizer as optim
import megengine.autodiff as autodiff

gm = autodiff.GradManager().attach(model.parameters())
optimizer = optim.SGD(
    model.parameters(),
    lr=0.01,
    momentum=0.9,
    weight_decay=5e-4
)

接下来训练我们的模型：将训练数据集分批地喂入模型，前向计算得到预测值， 根据设计好的损失函数（本教程中使用交叉熵 cross_entropy ）计算。 接着调用 GradManager.backward 方法来自动进行反向计算并记录梯度信息， 然后根据这些梯度信息来更新模型中的参数，即调用 Optimizer.step 方法。

import megengine


epochs = 10
model.train()
for epoch in range(epochs):
    total_loss = 0
    for batch_data, batch_label in train_dataloader:
        batch_data = megengine.Tensor(batch_data)
        batch_label = megengine.Tensor(batch_label)

        with gm:
            logits = model(batch_data)
            loss = F.nn.cross_entropy(logits, batch_label)
            gm.backward(loss)
            optimizer.step().clear_grad()

        total_loss += loss.item()

    print(f"Epoch: {epoch}, loss: {total_loss/len(train_dataset)}")

警告

记得将数据转为 MegEngine Tensor 格式，参考 深入理解 Tensor 数据结构 。

参见

想要了解更多细节，可以参考 Autodiff 基本原理与使用 / 使用 Optimizer 优化参数 。

测试：评估模型性能

在测试集上验证一下我们刚才训练好的 LeNet 模型的性能：

model.eval()
correct, total = 0, 0
for batch_data, batch_label in test_dataloader:
    batch_data = megengine.Tensor(batch_data)
    batch_label = megengine.Tensor(batch_label)

    logits = model(batch_data)
    pred = F.argmax(logits, axis=1)
    correct += (pred == batch_label).sum().item()
    total += len(pred)

print(f"Correct: {correct}, total: {total}, accuracy: {float(correct)/total}")

通常会得到一个在测试集上接近甚至超过 99% 预测正确率的模型。

注：通常的训练流程中应当使用验证集，每训练一段时间就及时验证，这里简化了这一步。

推理：用单张图片验证

我们也可以选择使用自己的手写数字图片来验证模型效果（你可以选择使用自己的图片）：

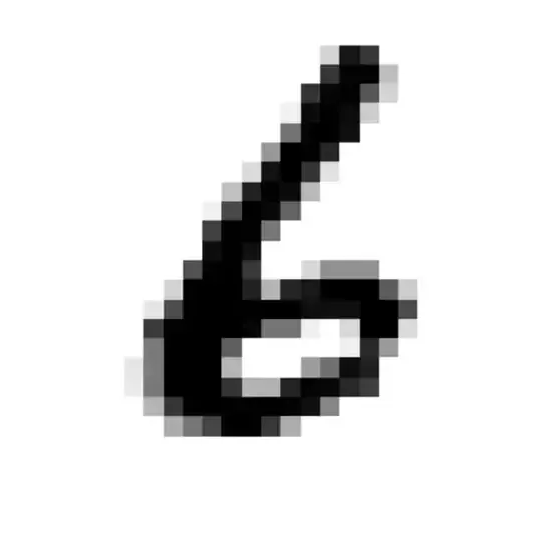
import cv2
import numpy as np

def process(image):
    image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    image = cv2.resize(image, (32, 32))
    image = np.array(255 - image)
    return image

image = cv2.imread("/data/handwrittern-digit.png")
processed_image = process(image)

这里为什么需要进行预处理

我们训练好的模型要求输入图片是形状为 32x32 的灰度图（单通道），且黑白底色要对应。 比如将白底黑字变换成黑底白字，就会对 255 这个值求差（因为表示范围为 [0, 255] ）。

上面是针对输入图片样本所做的一些必要预处理步骤，接下来将其输入模型进行推理：

>>> logit = model(megengine.Tensor(processed_image).reshape(1, 1, 32, 32))
>>> pred = F.argmax(logit, axis=1).item()
>>> pred
6

可以发现，我们训练出的 LeNet 模型成功地将手写该数字图片的标签类别预测为 6 ！

参见

这里展示的是最简单的模型推理情景，MegEngine 是一个训练推理一体化的框架， 能将训练好的模型导出，在 C++ 环境下高效地进行推理部署，可参考 模型部署总览与流程建议 中的介绍。

接下来做些什么？

我们已经成功地使用 MegEngine 框架完成了手写数字分类任务，很简单吧~

文档中还提供了更多内容

如果你对整个机器学习（深度学习）的流程依旧不是很清楚，导致阅读本教程有些吃力，不用担心。 我们准备了更加基础的 《 MegEngine 深度学习入门教程 》—— 它可以看作是当前教程内容的手把手教学版本，补充了更多细节和概念解释。 将从机器学习的基本概念开始讲起，循序渐进地帮助你理解整个开发流程， 在接触到更多经典模型结构的同时，也会更加了解如何使用 MegEngine 框架。 一些像是 保存与加载模型（S&L） 和 使用 Hub 发布和加载预训练模型 的用法，也会在该系列教程中进行简单介绍。

同时，由于这仅仅是一份快速上手教程，许多模型开发的进阶特性没有进行介绍，例如 分布式训练（Distributed Training） / 量化（Quantization） … 等专题，可以在 用户指南 中找到。 值得一提的是，MegEngine 不仅仅是一个深度学习训练框架，同时也支持便捷高效的模型推理部署。 关于模型推理部署的内容，可以参考 模型部署总览与流程建议 页面的介绍与 《 MegEngine 模型推理部署教程 》。

任何人都可以成为 MegEngine 教程的贡献者

由于开发者视角所带来的一些局限性，我们无法做到完全以用户视角来撰写文档中的各块内容，尽善尽美是长期追求。 如果你在阅读 MegEngine 教程的过程中产生了疑惑，或是有任何的建议，欢迎你加入 MegEngine 文档建设中来。

参考 如何为文档做贡献 页面了解更多细节。

参考文献

[1]

Yann LeCun, Corinna Cortes, and CJ Burges. Mnist handwritten digit database. ATT Labs [Online]. Available: http://yann.lecun.com/exdb/mnist, 2010.

[2]

Yann LeCun, Léon Bottou, Yoshua Bengio, and Patrick Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.