MegEngine 实现卷积神经网络#

本教程涉及的内容

理解 3 通道彩色图片与对应的 Tensor 表示，认识 Tensor 内存布局形式；
结合计算机视觉传统领域知识，在神经网络中使用 2D 卷积（Convolution）算子；
根据前面的介绍，使用 MegEngine 实现卷积神经网络，完成 CIFAR-10 图片分类任务。

警告

从本篇教程开始，模型更为复杂，训练时计算量将变得巨大，建议使用 GPU 环境运行代码。

获取原始数据集#

CIFAR-10 数据集与 MNIST 一样，可以直接通过 data.dataset 来获取：

from megengine.data.dataset import CIFAR10
from os.path import expanduser

DATA_PATH = expanduser("~/data/datasets/CIFAR10")

train_dataset = CIFAR10(DATA_PATH, train=True)
test_dataset = CIFAR10(DATA_PATH, train=False)

与 MNIST 的处理类似，此处得到的是已经划分好的训练集和测试集，且都封装成了 MegEngine 中的 Dataset 类型，为了方便进行分析，我们这里将其转换成 NumPy 的 ndarray 数据格式：

import numpy as np

X_train, y_train = map(np.array, train_dataset[:])

>>> print(X_train.shape, y_train.shape)
(50000, 32, 32, 3) (50000,)

了解数据集信息#

可以发现，CIFAR-10 中每个图片样本的形状为 $(32, 32, 3)$, 与 MNIST 数据集中形状为 $(28, 28, 1)$ 的样本的高度、高度、以及 通道（Channel） 数量都有差异，让我们进一步了解 CIFAR-10 的样本信息：

3 通道 RGB 图片#

RGB 颜色模型（RGB color model）

RGB 颜色模型或红绿蓝颜色模型，是一种加色模型，将红（Red）、绿（Green）、蓝（Blue）三原色的色光以不同的比例相加，以合成产生各种色彩光。（下图来自维基百科， CC-BY-SA 4.0）

RGB 颜色模型的主要目的是在电子系统中检测、表示和显示图像，比如电视和电脑，利用大脑强制视觉生理模糊化（失焦），将红绿蓝三原色子象素合成为一色彩象素，产生感知色彩。其实此真彩色并非加色法所产生的合成色彩，原因为该三原色光从来没有重叠在一起，只是人类为了 “想” 看到色彩，大脑强制眼睛失焦而形成。三原色的原理不是出于物理原因，而是由于生理原因造成的。

阅读官网和文档的说明很重要，CIFAR10 主页上的原始数据是以 RGB 顺序存储的，而 MegEngine 中的 CIFAR10 接口在处理数据时，会有一个将原本 RGB 顺序变为 BGR 顺序的操作，从而得到 BGR 通道顺序的数据。

相较于单通道图片，我们在做归一化处理时，需要每个通道分别计算相应的统计量，这里提前统计好：

>>> mean = [X_train[:,:,:,i].mean() for i in range(3)]
>>> mean
[113.86538318359375, 122.950394140625, 125.306918046875]

>>> std = [X_train[:,:,:,i].std() for i in range(3)]
>>> std
[66.70489964063091, 62.08870764001421, 62.993219278136884]

查询 transform.Normalize API 文档你会发现，它能够接受上述 mean 和 std 作为输入，用于每个通道。

图片 Tensor 布局#

目前的 CIFAR10 数据集中，每张图片的形状为 $(32, 32, 3)$, 又称为 HWC 布局（Layout）或格式（Mode）。但在 MegEngine 中，处理 3 通道图像 Tensor 数据的绝大部分算子都要求默认为 CHW 布局输入（目前不用了解原因），因此我们在预处理的最后一步，还需要对图片数据做 Layout 的变换，用到 ToMode 接口：

from megengine.data.transform import ToMode

sample = X_train[0]
trans_sample = ToMode().apply(sample)

>>> print(sample.shape, trans_sample.shape)
(32, 32, 3) (3, 32, 32)

备注

再次提醒，此时的数据依旧是 ndarray 格式，通常在提供给模型时才会被转换成 Tensor 格式。

参见

更多的预处理阶段的变换操作，可参考使用 Transform 定义数据变换；
更多对 Layout 的介绍，可参考 Tensor 内存布局页面的介绍。

但对于全连接神经网络，不论是 CHW 布局还是 HWC 布局，使用线性层，其经过 flatten 后进行线性运算，只会得到排列顺序不同的神经元，最终产生的效果是一样的，接下来我们将看看全连接神经网络有什么不足。

再次思考 flatten 处理#

CIFAR10 数据集 + 全连接神经网络

我们使用上一个教程中的全连接神经网络在 CIFAR10 上进行训练（源码在 examples/beginner/neural-network-cifar10.py ），这里直接使用提前统计好的均值和标准差进行归一化：

import megengine
import megengine.data as data
import megengine.data.transform as T
import megengine.functional as F
import megengine.module as M
import megengine.optimizer as optim
import megengine.autodiff as autodiff

from os.path import expanduser
DATA_PATH = expanduser("~/data/datasets/CIFAR10")

train_dataset = data.dataset.CIFAR10(DATA_PATH, train=True)
test_dataset = data.dataset.CIFAR10(DATA_PATH, train=False)

train_sampler = data.RandomSampler(train_dataset, batch_size=64)
test_sampler = data.SequentialSampler(test_dataset, batch_size=64)

"""
import nump as np

X_train, y_train = map(np.array, train_dataset[:])
mean = [X_train[:,:,:,i].mean() for i in range(3)]
std = [X_train[:,:,:,i].std() for i in range(3)]
"""

transform = T.Normalize([113.86538318359375, 122.950394140625, 125.306918046875],
                        [66.70489964063091, 62.08870764001421, 62.993219278136884])

train_dataloader = data.DataLoader(train_dataset, train_sampler, transform)
test_dataloader = data.DataLoader(test_dataset, test_sampler, transform)

num_features = train_dataset[0][0].size
num_hidden = 256
num_classes = 10


# Define model
class NN(M.Module):
    def __init__(self):
        super().__init__()
        self.fc = M.Linear(num_features, num_hidden)
        self.classifier = M.Linear(num_hidden, num_classes)

    def forward(self, x):
        x = F.nn.relu(self.fc(x))
        x = self.classifier(x)
        return x


model = NN()

# GradManager and Optimizer setting
gm = autodiff.GradManager().attach(model.parameters())
optimizer = optim.SGD(model.parameters(), lr=0.01)


# Training and validation
nums_epoch = 50
for epoch in range(nums_epoch):
    training_loss = 0
    nums_train_correct, nums_train_example = 0, 0
    nums_val_correct, nums_val_example = 0, 0

    for step, (image, label) in enumerate(train_dataloader):
        image = F.flatten(megengine.Tensor(image), 1)
        label = megengine.Tensor(label)

        with gm:
            score = model(image)
            loss = F.nn.cross_entropy(score, label)
            gm.backward(loss)
            optimizer.step().clear_grad()

        training_loss += loss.item() * len(image)

        pred = F.argmax(score, axis=1)
        nums_train_correct += (pred == label).sum().item()
        nums_train_example += len(image)

    training_acc = nums_train_correct / nums_train_example
    training_loss /= nums_train_example

    for image, label in test_dataloader:
        image = F.flatten(megengine.Tensor(image), 1)
        label = megengine.Tensor(label)
        pred = F.argmax(model(image), axis=1)

        nums_val_correct += (pred == label).sum().item()
        nums_val_example += len(image)

    val_acc = nums_val_correct / nums_val_example

    print(f"Epoch = {epoch}, "
          f"train_loss = {training_loss:.3f}, "
          f"train_acc = {training_acc:.3f}, "
          f"val_acc = {val_acc:.3f}")

我们在上一个教程中定义的全连接神经网络结构，在 CIFAR10 上仅仅能够取得 50% 左右的分类准确率，意味着不合格。神经网络模型中还存在着除全连接以外的计算模式，在处理不同类型的任务和数据时，能产生不同的效果。这就要求我们对任务和数据有着更深的理解和思考，而不是完全寄希望于加深网络结构，调整超参数。

备注

全连接神经网络不能够很好地应用于分辨率更高的图像数据。更大尺寸的图像会导致全连接网络中的神经元数量变得更多，这意味着模型中的 参数量 和训练时的 计算量 会变得巨大，成本可能无法接受；另外，大量的参数可能会导致模型训练时很快产生过拟合现象。
全连接神经网络的输入必须是一个展平后的特征向量，因此我们之前采取的处理是 flatten 操作，并没有考虑可能产生的影响。这样的操作可以看作是对图片数据进行了一次降维，会丢失掉非常多的信息 —— 比如各个相邻居像素之间的局部 空间信息 。
全连接神经网络对图像中像素位置的变化比较敏感，两张图片如果彼此之间的差异仅仅是做了些上下平移，对全连接神经网络而言就可能会认为这些空间信息已经截然不同，不具备空间 平移不变性 。

让我们从传统计算机视觉领域获得一些启发，是人们是如何利用图片的空间信息的。

数字图像处理：滤波#

数字图像处理（Digital Image Processing）是通过计算机对图像进行去除噪声、增强、复原、分割、提取特征等处理的方法和技术。本教程中不会对这个领域进行过多的介绍，而将专注于介绍其中的滤波（Filtering）和卷积（Convolution）操作。首先让我们使用 OpenCV 中的 cv2.filter2D 接口，来有一个直观的认识：

image_path = "/path/to/example.jpg"  # Select the same image to read
image = plt.imread(image_path)

filters = [np.array([[  0,  0,  0],
                     [  0,  1,  0],
                     [  0,  0,  0]]),
           np.array([[ -1, -2, -1],
                     [  0,  0,  0],
                     [  1,  2,  1]]),
           np.array([[  0, -1,  0],
                     [ -1,  8, -1],
                     [  0, -1,  0]])]

for idx, filter in enumerate(filters):
    result = cv2.filter2D(image, -1, filter)
    plt.subplot(1,3,idx+1)
    plt.axis('off')
    plt.imshow(result)
plt.show()

注： cv2.filter2D 中的 -1 表示自动地将滤波器矩阵应用到图片的每个通道。

可以直观地感受到，滤波操作能够对图像的特征进行很好地处理。其步骤是：即首先对原图周围进行 0 值填充，然后计算图像中每个像素的邻域像素矩阵和滤波器矩阵的对应乘积，然后求和作为该像素位置的值。作为验证，像素和我们上面的第一个滤波器矩阵进行计算，得到的还是原始值，因此最终的输出为原图。

在滤波过程中利用了图片的空间信息，且使用不同的滤波器将得到不同的效果，如边缘提取、模糊、锐化等等。

理解卷积算子#

滤波操作可以理解成是填充（Padding）与卷积（Convolution）操作的结合：

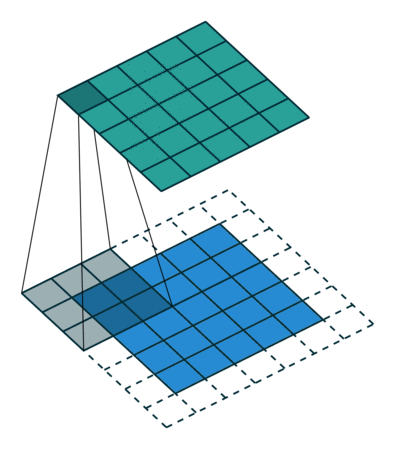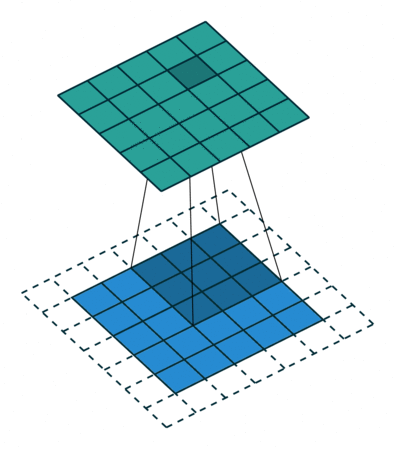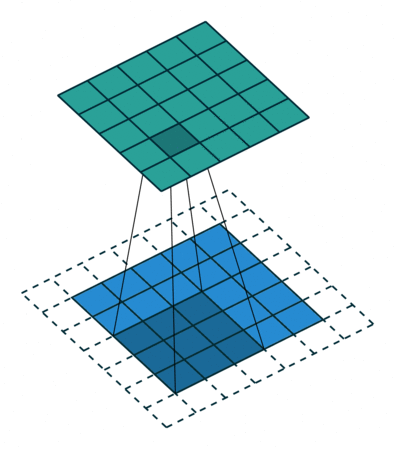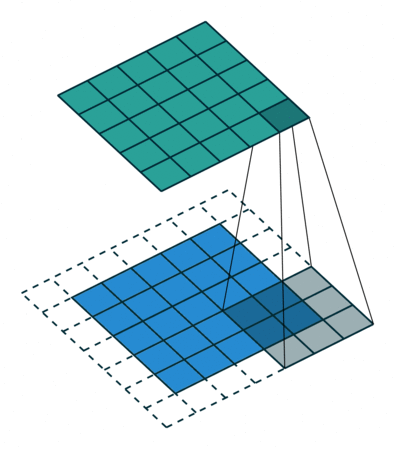
../../_images/convolution-animation-1.gif

以上图为例子，帮助我们更好地理解卷积计算的过程。图中的蓝色部分（底部）表示输入通道，蓝色部分上的阴影表示 $3 \times 3$ 卷积核（Kernel），绿色部分（顶部）表示输出通道。对于蓝色输入通道上的每个位置，都会进行卷积运算，即将蓝色输入通道的阴影部分映射到绿色输出通道的相应阴影部分。

在 CIFAR10 中，输入图像为 3 通道的，因此我们需要使用形状为 $3 \times 3 \times 3$ 的卷积核，卷积核深度为 3 意味着卷积核中有 3 个不同的滤波器与每个通道分别进行计算，同一位置不同通道计算出的值相加，最终依旧会得到一个形状为 $32 \times 32$ 的 2D 输出（假定填充宽度为 1），我们称之为特征图（Feature map）。

备注

在 MegEngine 中实现的对应 Tensor 操作接口为 pad 和 conv2d （在调用 conv2d 时可通过 padding 参数达到同样的效果），后者即对图像这种形式的 Tensor 数据进行 2D 卷积操作的接口，其对应的 Module 为 Conv2d. 在 Conv2d 中还有着：步幅（Stride），表示每次滤波器移动的距离；以及还有 dilation, groups 等等参数，输入需要为 NCHW 布局，具体说明请查阅 API 文档。

警告

严格来说，深度学习中所指的输入数据和卷积核之间执行的这种运算过程其实是互相关（Cross-correlation）运算，而不是卷积运算（真实的卷积运算需要先将卷积核沿对角线翻转），而我们通常不采用互相关这个说法，习惯称之为卷积。

下面来看一个在 MegEngine 中使用卷积运算的例子：

from megengine import Tensor
from megengine.module import Conv2d

sample = X_train[:100]  # NHWC
batch_image = Tensor(sample, dtype="float32").transpose(0, 3, 1, 2)  # NCHW

>>> batch_image.shape
(100, 3, 32, 32)

>>> result = Conv2d(3, 10, (3, 3), stride=1, padding=1)(batch_image)
>>> result.shape
(100, 10, 32, 32)

可以发现，我们的通道数由 3 变为了 10，如果改变 stride 和 padding 参数的设置，输出特征图的高度和宽度也会改变，这一点和滤波操作是不一样的。而相较于全连接层，卷积层中的每个神经元在计算时只关注自己感兴趣的部分，更加能利用图像的空间信息。卷积操作可以理解成是一种特征提取操作，能够从图像中学得信息。

卷积神经网络架构模式

目前最为流行的卷积神经网络架构模式为 ——

[Conv->Actication->Pooling]->flatten->[Linear->Actication]->Score.

在神经网络中，想要为模型引入非线性，需要在计算完成后加入激活函数，卷积层也一样；
另外在使用卷积层对特征完成提取后，通常还会使用 MaxPool2d 等池化（Pooling）操作。其逻辑是沿着空间维度（高度、宽度）执行下采样操作，即一片区域中仅仅保留一块局部信息作为代表。一种解释是，这样的操作能够使得卷积神经网络模型能够具有更好的泛化能力；它逐步减少了图像空间的大小，以减少网络中的参数量和计算量，从而控制了过拟合。
当使用卷积层提取到足够原始的特征后，便可以像 MNIST 数据一样使用全连接层进行分类。

此处的介绍有些简略，更加详细的解释可以参考 Stanford CS231n 课程的官方笔记。

练习：卷积神经网络#

接下来我们要做的事情是 “看图说话”，实现一个卷积神经网络并对 CIFAR10 进行分类：

我们参考的是 LeNet [2] 网络，其模型的结构如下图所示（图片截取自论文）：

../../_images/lenet5.png — Architecture of LeNet a Convolutional Neural Network here for digits recognition. Each plane is a feature map ie a set of units whose weights are constrained to be identical.#

注意：我们在数据预处理时使用了 Compose 来对各种变换进行组合。

import megengine
import megengine.data as data
import megengine.data.transform as T
import megengine.functional as F
import megengine.module as M
import megengine.optimizer as optim
import megengine.autodiff as autodiff


from os.path import expanduser
DATA_PATH = expanduser("~/data/datasets/CIFAR10")

train_dataset = data.dataset.CIFAR10(DATA_PATH, train=True)
test_dataset = data.dataset.CIFAR10(DATA_PATH, train=False)

train_sampler = data.RandomSampler(train_dataset, batch_size=64)
test_sampler = data.SequentialSampler(test_dataset, batch_size=64)

"""
import nump as np

X_train, y_train = map(np.array, train_dataset[:])
mean = [X_train[:,:,:,i].mean() for i in range(3)]
std = [X_train[:,:,:,i].std() for i in range(3)]
"""

transform = T.Compose([
    T.Normalize([113.86538318359375, 122.950394140625, 125.306918046875],
                [66.70489964063091, 62.08870764001421, 62.993219278136884]),
    T.ToMode("CHW"),
])

train_dataloader = data.DataLoader(train_dataset, train_sampler, transform)
test_dataloader = data.DataLoader(test_dataset, test_sampler, transform)


# Define model
class ConvNet(M.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = M.Conv2d(3, 6, 5)
        self.conv2 = M.Conv2d(6, 16, 5)
        self.fc1 = M.Linear(16*5*5, 120)
        self.fc2 = M.Linear(120, 84)
        self.classifier = M.Linear(84, 10)

        self.relu = M.ReLU()
        self.pool = M.MaxPool2d(2, 2)

    def forward(self, x):
        x = self.pool(self.relu(self.conv1(x)))
        x = self.pool(self.relu(self.conv2(x)))
        x = F.flatten(x, 1)
        x = self.relu(self.fc1(x))
        x = self.relu(self.fc2(x))
        x = self.classifier(x)
        return x


model = ConvNet()

# GradManager and Optimizer setting
gm = autodiff.GradManager().attach(model.parameters())
optimizer = optim.SGD(model.parameters(), lr=0.01)


# Training and validation
nums_epoch = 50
for epoch in range(nums_epoch):
    training_loss = 0
    nums_train_correct, nums_train_example = 0, 0
    nums_val_correct, nums_val_example = 0, 0

    for step, (image, label) in enumerate(train_dataloader):
        image = megengine.Tensor(image)
        label = megengine.Tensor(label)

        with gm:
            score = model(image)
            loss = F.nn.cross_entropy(score, label)
            gm.backward(loss)
            optimizer.step().clear_grad()

        training_loss += loss.item() * len(image)

        pred = F.argmax(score, axis=1)
        nums_train_correct += (pred == label).sum().item()
        nums_train_example += len(image)

    training_acc = nums_train_correct / nums_train_example
    training_loss /= nums_train_example

    for image, label in test_dataloader:
        image = megengine.Tensor(image)
        label = megengine.Tensor(label)
        pred = F.argmax(model(image), axis=1)

        nums_val_correct += (pred == label).sum().item()
        nums_val_example += len(image)

    val_acc = nums_val_correct / nums_val_example

    print(f"Epoch = {epoch}, "
          f"train_loss = {training_loss:.3f}, "
          f"train_acc = {training_acc:.3f}, "
          f"val_acc = {val_acc:.3f}")

经过接近 50 轮训练，通常能够得到一个准确率超过 60% 的 LeNet 模型，比单纯使用全连接神经网络要好一些。

在本教程中，向你介绍了卷积神经网络的基本概念，并且使用 LeNet 模型在 CIFAR10 数据集上进行了训练和评估。实际上，LeNet 模型在 MNIST 数据集上能够取得超过 99% 的分类准确率，这也是我们在《MegEngine 快速上手》中给出的例子，你现在应当能够完全理解这个教程了。

参见

本教程的对应源码： examples/beginner/linear-classification.py

总结：炼丹不完全是玄学#

深度学习领域，模型是丹方，数据是灵材，GPU 设备是三昧真火，而 MegEngine 则是强大的炼丹炉。

作为炼丹人员，或许在 “调参” 这一步确实会花费掉非常多的时间，且总是会发生一些玄学现象。但经过这一系列教程，相信你也认识到了一些更深层次的内容，让我们再次回顾一下机器学习的概念：

A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.

如果一个计算机程序能够根据经验 E 提升在某类任务 T 上的性能 P, 则我们说程序从经验 E 中进行了学习。

在指导机器进行学习的过程中，我们对经验、任务和性能需要有更加深刻的理解：

经验：深度学习的模型经验通常来自于数据集和损失（从犯错中学习）。在本教程中没有涉及到太多关于数据标采、预处理等相关的知识，然而在实际工程实践中，数据的质量也十分关键，越多的数据通常能带来越好的性能。设计科学的损失函数也很重要，它直接决定了我们的优化目标。
任务：很多时候，传统领域的知识会给我们带来很多的其它，机器在一些任务上能做得比人类更高效；
性能：我们对于不同的任务会选用评估指标，本系列教程中介绍的只是冰山一角。