MegEngine 实现神经网络#
本教程涉及的内容
思考线性模型的局限性,考虑如何解决线性不可分问题,引出 “激活函数” 的概念;
对神经元(Neural)以及全连接(Fully connected)网络模型结构有一个基本理解;
接触到不同的参数初始化策略,学会使用
module模块提升模型设计效率;根据前面的介绍,使用 MegEngine 实现两层全连接神经网络,完成 Fashion-MNIST 图片分类任务。
获取原始数据集#
在上一个教程中,我们使用了 MegEngine 的 data.dataset 模块来获取 MNIST 数据集,
并使用线性分类器取得了超过 90% 的分类准确率。接下来我们将在与之类似的 Fashion-MNIST 数据集上,
使用完全一样的模型结构和优化策略,看线性模型是否依旧能取得一样出色的效果。
通常经过 5 轮训练,使用线性分类器(Logistic 回归模型)在 Fashion-MNIST 上能达到 83% 的准确率。
Fashion-MNIST 数据集 + 线性分类器
Fashion-MNIST [1] 是一个替代MNIST手写数字集的图像数据集。它是由 Zalando(一家德国的时尚科技公司)旗下的研究部门提供。 其涵盖了来自 10 种类别的共 7 万个不同商品的正面图片。Fashion-MNIST 的大小、格式和训练集/测试集划分与原始的 MNIST 完全一致。 60000/10000的 训练测试数据划分,28x28 的灰度图片。你可以直接用它来测试你的机器学习和深度学习算法性能, 且 不需要 改动任何的代码。
这一部分的源码可以在 examples/beginner/linear-classification-fashion.py 找到,区别在于:
MegEngine 在
data.dataset模块提供了MNIST接口,而 Fashion-MNIST 需要手动下载;借助下面的
load_mnist函数得到 ndarray 格式的数据集,需要借助ArrayDataset进行封装。
import megengine
import megengine.data as data
import megengine.data.transform as T
import megengine.functional as F
import megengine.optimizer as optim
import megengine.autodiff as autodiff
def load_mnist(path, kind='train'):
import os
import gzip
import numpy as np
"""Load MNIST data from `path`"""
labels_path = os.path.join(path,
'%s-labels-idx1-ubyte.gz'
% kind)
images_path = os.path.join(path,
'%s-images-idx3-ubyte.gz'
% kind)
with gzip.open(labels_path, 'rb') as lbpath:
labels = np.frombuffer(lbpath.read(), dtype=np.uint8,
offset=8)
with gzip.open(images_path, 'rb') as imgpath:
images = np.frombuffer(imgpath.read(), dtype=np.uint8,
offset=16).reshape(len(labels), 784)
return images, labels
# Get train and test dataset and prepare dataloader
# Make sure that you have downloaded data and placed it in `DATA_PATH`
# GitHub link: https://github.com/zalandoresearch/fashion-mnist
from os.path import expanduser
DATA_PATH = expanduser("~/data/datasets/Fashion-MNIST")
X_train, y_train = load_mnist(DATA_PATH, kind='train')
X_test, y_test = load_mnist(DATA_PATH, kind='t10k')
mean, std = X_train.mean(), X_train.std()
train_dataset = data.dataset.ArrayDataset(X_train, y_train)
test_dataset = data.dataset.ArrayDataset(X_test, y_test)
train_sampler = data.RandomSampler(train_dataset, batch_size=64)
test_sampler = data.SequentialSampler(test_dataset, batch_size=64)
transform = T.Normalize(mean, std)
train_dataloader = data.DataLoader(train_dataset, train_sampler, transform)
test_dataloader = data.DataLoader(test_dataset, test_sampler, transform)
num_features = train_dataset[0][0].size
num_classes = 10
# Parameter initialization
W = megengine.Parameter(F.zeros((num_features, num_classes)))
b = megengine.Parameter(F.zeros((num_classes,)))
# Define linear classification model
def linear_cls(X):
return F.matmul(X, W) + b
# GradManager and Optimizer setting
gm = autodiff.GradManager().attach([W, b])
optimizer = optim.SGD([W, b], lr=0.01)
# Training and validation
nums_epoch = 5
for epoch in range(nums_epoch):
training_loss = 0
nums_train_correct, nums_train_example = 0, 0
nums_val_correct, nums_val_example = 0, 0
for step, (image, label) in enumerate(train_dataloader):
image = F.flatten(megengine.Tensor(image), 1)
label = megengine.Tensor(label).astype("int32")
with gm:
score = linear_cls(image)
loss = F.nn.cross_entropy(score, label)
gm.backward(loss)
optimizer.step().clear_grad()
training_loss += loss.item() * len(image)
pred = F.argmax(score, axis=1)
nums_train_correct += (pred == label).sum().item()
nums_train_example += len(image)
training_acc = nums_train_correct / nums_train_example
training_loss /= nums_train_example
for image, label in test_dataloader:
image = F.flatten(megengine.Tensor(image), 1)
label = megengine.Tensor(label).astype("int32")
pred = F.argmax(linear_cls(image), axis=1)
nums_val_correct += (pred == label).sum().item()
nums_val_example += len(image)
val_acc = nums_val_correct / nums_val_example
print(f"Epoch = {epoch}, "
f"train_loss = {training_loss:.3f}, "
f"train_acc = {training_acc:.3f}, "
f"val_acc = {val_acc:.3f}")
可以借助下面的代码直接对比两个源码文件之间的区别:
cd examples/beginner
diff linear-classification.py linear-classification-fashion.py
这样的结果相较于人类水平其实并不算理想,我们需要设计出更好的机器学习模型。
线性模型的局限性#
线性模型比较简单,因此也存在着诸多局限性。 比如处理分类问题时,其生成的决策边界是一个超平面, 这意味着理想情况下,样本点在特征空间中是线性可分的。 最典型的反例是,它无法解决异或(XOR)运算问题:
四个样本组成的数据集
输入 \(\boldsymbol{x}_i\) |
特征 \(x_{i1}\) |
特征 \(x_{i2}\) |
输出 \(y_i\) |
|---|---|---|---|
\(\boldsymbol{x}_1\) |
0 |
0 |
0 |
\(\boldsymbol{x}_2\) |
0 |
1 |
1 |
\(\boldsymbol{x}_3\) |
1 |
0 |
1 |
\(\boldsymbol{x}_4\) |
1 |
1 |
0 |
二维空间表示
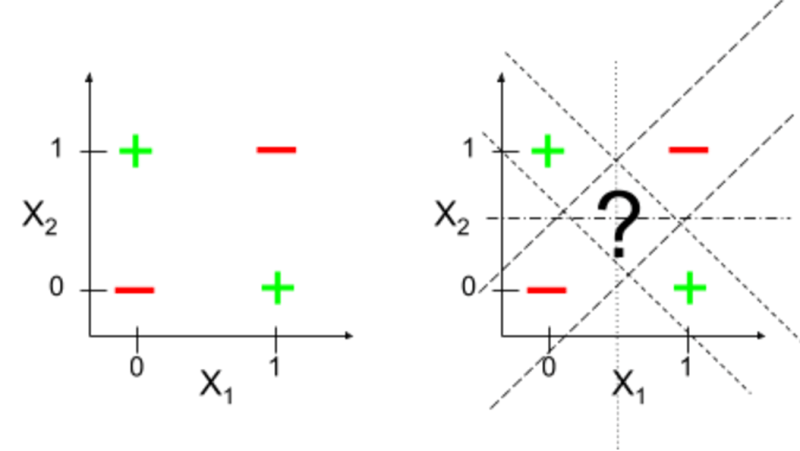
由于数据线性不可分,我们找不到这样一个线性决策边界,能够将这两类样本很好地分隔开。
备注
我们即将从线性模型过渡到神经网络模型,你会发现一切早已悄然发生。
引入非线性因素#
回忆一下,在上一个教程中,我们的线性分类器在前向计算时会有一个将线性预测映射到概率值的操作(链接函数)。 由于这一步计算对模型中样本的决策边界并没有影响,因此我们依旧可以认为这是广义线性模型(更术语的解释是, 我们对观测到的样本假设依旧服从某个指数族分布,本教程不会介绍太多的数学细节)。
是时候告诉你一个秘密了:线性模型本身其实可以被看做是最简单的单层神经网络!
如果将 MNIST 图片样本展平后的特征向量 \(\boldsymbol{x}\) 看作是输入层(Input Layer), 那么对于二分类问题,我们可以当做这里有一个神经元,负责完成线性预测 \(z=\boldsymbol{w}^T \boldsymbol{x} + b\) 和链接函数 \(a=\sigma(z)\) 相关的计算。 在二分类问题中,输出层(Output Layer)只要一个神经元就可以完成工作,多分类问题则需要多个神经元。#
神经元计算模型,与生物学的联系
大脑的基本计算单元是神经元(Neuron)。在人类神经系统中可以发现大约 860 亿个神经元, 它们与大约 \(10^{14}\) ~ \(10^{15}\) 个突触(Synapses)相连。 下图显示了生物神经元(左)和常见数学模型(右)的示例。 每个神经元从其树突(Dendrites)接收输入信号,并沿其唯一的轴突(Axon)产生输出信号。 轴突最终分支出来并通过突触连接到其它神经元的突触。在神经元计算模型中, 沿着轴突传播的信号(如 \(x_0\) )将基于突触的突触强度(如 \(w_0\) ) 与其它神经元的树突进行乘法交互(如 \(w_0 x_0\))。突触强度(也就是权重 \(w\) ) 是可学习的,且可以控制一个神经元对另一个神经元的影响程度(以及可以控制方向, 比如正权重代表兴奋,负权重代表抑制)。在基本模型中,树突将信号传递到细胞体,信号在细胞体中相加。 如果最终之和高于某个阈值,那么神经元将会 激活(Activation) ,向其轴突输出一个峰值信号。
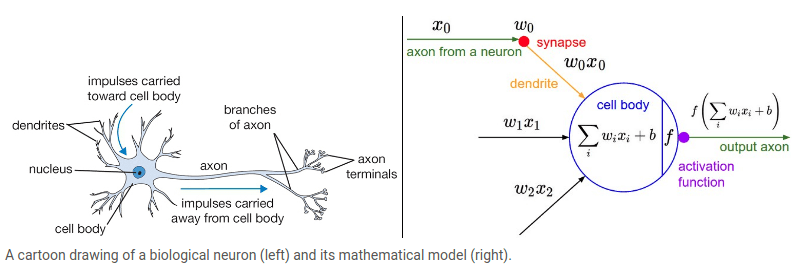
(注:本段解释和图片引用自 CS231n 讲义中的 部分材料 。)
多分类问题,即意味着最终由多个神经元计算多个输出
激活函数与隐藏层#
在神经元计算模型中,非线性函数被称为激活函数(Activation function), 历史上常被使用的激活函数即我们见过的 Sigmoid 函数 \(\sigma(\cdot)\). 这给我们带来了启发,激活函数是非线性的,这也意味着通过多个神经元突触之间的连接,给我们的计算模型引入了非线性。 我们可以通过引入一个隐藏层(Hidden Layer)来做到这一点:
隐藏层中带有 12 个神经元,每个神经元需要负责进行相应的非线性计算,决定是否激活。#
我们来规范一下术语,在神经网络模型中,上面的神经网络被称为 2 层全连接神经网络。 输入层是样本特征,不发生实际计算,因此不算入模型层数。 隐藏层可以有多个,每层的神经元个数需要人为设定。 由于线性层的神经元是与上一层的所有输入完全连接在一起的,因此也叫做全连接层(Full connected layer, FC Layer)。 正是因为在全连接层后面加上激活函数,借此让神经网络具有了非线性计算的能力。
使用 MegEngine 来模拟一下这个计算过程,直觉感受一下(这里只关注形状变化):
x = F.ones((16,))
W1 = F.zeros((16, 12))
b1 = F.zeros((12,))
z1 = F.matmul(x, W1) + b1 # Linear (full connected)
a1 = F.nn.sigmoid(z1) # Activations
W2 = F.zeros((12, 10))
b2 = F.zeros((10))
z2 = F.matmul(a1, W2) + b2 # Linear (full connected)
output = F.softmax(z2) # Logits
>>> output.shape
(10,)
在 MegEngine 中,常见的非线性激活函数被实现在 functional.nn 模块中。
由于神经网络中可能存在着大量的非线性计算,又不像分类器一样要求输出映射到概率区间,
因此更加常用的激活函数是 relu 函数等,全称修正线性单元(Rectified linear unit,ReLU)。
相较于 sigmoid 函数,它有着计算和求导简单的特点,又满足非线性计算的特性要求。
更加具体的解释,可以查看不同激活函数的 API 文档。
深度学习领域,有许多针对激活函数的研究和设计,在本教程中方便起见,均使用 ReLU 激活函数。
多层神经网络#
除了激活函数的选用,定义全连接神经网络的步骤主要在设计隐藏层层数和每层神经元的个数。
我们可以通过堆叠更多的隐藏层,使得模型具有更强的学习能力和表达能力。 从这个角度来看,线性模型中的变换(准确来说是仿射变换,但在这里我们强调的是非线性和线性的区别) 不论如何叠加,最终都可以用等效的变换来表示,即矩阵运算中 \(C=AB\) 的形式。 尽管我们通过激活函数引入了非线性,但问题也随之出现了:
我们需要对更多的模型参数进行管理,本教程中会给出 MegEngine 中的解决方案;
神经网络模型理论上可以逼近任意函数,使用更深的网络通常意味着更强的近似能力。 但我们不能胡乱设计,还需要对模型中的参数量(计算量)以及模型最终的性能之间进行权衡取舍。
参见
目前接触到的这种仅由全连接层(与激活函数)组成神经网络模型架构, 在某些材料中也被称为多层感知机(Multilayer perceptron, MLP)。 其出发点是针对感知机算法进行改进,进而得到了 MLP. 二者实质上指代相同。 我们解决二分类问题使用的是 Logistic 回归,因此没有采用感知机这种称呼。
随机初始化策略#
我们需要注意到全连接层的一些特点,比如层中的每一个神经元都会与前一层中所有输入进行运算。 回忆一下,我们在介绍线性模型时,提到了模型中的参数将从一个初始值不断地进行迭代优化, 并且采取了最简单的初始化策略,全零初始化,即将模型中所有参数的值初始化为 0. 这种做法在单层模型输出 + 损失函数的情况下是有效的,但对多层神经网络而言将导致问题。
假设我们将隐藏层中的所有神经元参数初始化为零,这其实意味着所有的神经元都在做同样的事情:
前向计算时,由于前一层的输入是同样的,因此同一层的神经元的前向计算的输出都将一样;
经过激活函数时,由于激活函数 ReLU 没有随机性,因此也会得到同样的输出,并传给下一层;
反向计算时,所有的参数将得到同样的梯度,在学习率一致的情况下,参数更新后也是一致的。
这就导致全连接层中的所有神经元都在做一样的事情,表达能力大大减弱。解决办法是,使用随机初始化策略。
MegEngine 生成随机数据
在 MegEngine 中提供了 random 模块来随机生成 Tensor 数据:
import megengine.random as rand
rand.seed(20200325)
x = rand.normal(0, 1, (3, 3))
>>> x
Tensor([[ 0.014 0.3366 0.877 ]
[ 0.4073 -0.0031 0.2638]
[-0.1826 1.4192 0.2758]], device=xpux:0)
其中 random.seed 可以设置一个随机种子,方便在一些情况下复现随机状态。
我们借助 normal 接口从标准正态分布(均值为 0, 标准差为 1)
中随机生成了形状为 \((3, 3)\) 的 Tensor.
当模型变复杂后,重复的编码模式出现了
假定我们需要在原来线性分类模型的基础上加入一层神经元个数为 256 的隐藏层:
num_features = train_dataset[0][0].size
num_hidden = 256
num_classes = 10
W1 = megengine.Parameter(rand.normal(0, 1, (num_features, num_hidden)))
b1 = megengine.Parameter(F.zeros((num_hidden,)))
W2 = megengine.Parameter(rand.normal(0, 1, (num_hidden, num_classes)))
b2 = megengine.Parameter(F.zeros((num_classes,)))
def model(X):
z1 = F.matmul(X, W1) + b1
a1 = F.nn.relu(z1)
z2 = F.matmul(a1, W2) + b2
return z2
gm = autodiff.GradManager().attach([W1, W2, b1, b2])
optimizer = optim.SGD([W1, W2, b1, b2], lr=0.1)
可以明显地感受到,当模型结构变得越来越复杂时,代码中将充斥着大量的重复性内容。
作为一个深度学习框架,MegEngine 自然需要提供一种方便的做法,来对模型进行设计。
使用 Module 定义模型#
参见
本教程这一小节的介绍比较精简,完整内容请参考 使用 Module 定义模型结构 。
MegEngine 中的 module 模块为神经网络模型中的结构提供了一类抽象机制,
一切均为 Module 类,除了为常见模块实现了默认的随机初始化策略外,
并提供了常见的方法(如即将介绍的 Module.parameters )。
这样可以方便用户专注于设计网络结构,从重复的参数初始化和管理方式等细节中解脱出来。
例如对于像 matmul 这样的线性层运算,可以使用 Linear 进行表示:
import megengine.module as M
x = F.ones((num_features,)) # (784,)
fc = M.Linear(num_features, num_hidden) # (784, 256)
可以发现 fc 模块中有着对应形状的权重(Weight)和偏置(Bias)参数,且自动完成了初始化。
>>> fc.weight.shape
(256, 784)
>>> fc.bias.shape
(256,)
查阅 API 文档可知,对于输入的样本 \(x\), 计算过程是 \(y=xW^T+b\).
简单验证一下 Linear 的运算结果,与 matmul 得到的结果是一致的(在浮点误差范围内):
>>> a = fc(x)
>>> b = F.matmul(x, fc.weight.transpose()) + fc.bias
>>> print(a.shape, b.shape)
(256,) (256,)
>>> a - b < 1e-6
Tensor([ True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True], dtype=bool, device=xpux:0)
Module 参数初始化策略
Linear 作为内置的 Module, 我们不需要人为地初始化,
该过程在其对应的 __init__ 方法中已经实现,也允许被用户自己的实现覆盖掉。
一些常见的初始化策略在 module.init 模块中进行了提供,在本教程中不会进行具体介绍。
Module 允许像搭积木一样进行嵌套实现,因此在本教程中的全连接神经网络可以这样实现:
所有网络结构都源自基类
M.Module. 在构造函数中,一定要先调用super().__init__().在构造函数中,声明要使用的所有层/模块;
在
forward函数中,定义模型将如何运行,从输入到输出。
class NN(M.Module):
def __init__(self):
super().__init__()
self.fc = M.Linear(num_features, num_hidden)
self.classifier = M.Linear(num_hidden, num_classes)
def forward(self, x):
x = F.nn.relu(self.fc(x))
x = self.classifier(x)
return x
可以借助 Module.parameters 得到模型的参数的迭代器,提供给梯度管理器和优化器:
>>> gm = autodiff.GradManager().attach(model.parameters())
>>> optimizer = optim.SGD(model.parameters(), lr=0.01)
练习:前馈神经网络#
前馈神经网络是一种最简单的神经网络,各神经元分层排列,每个神经元只与前一层的神经元相连。 接收前一层的输出,并输出给下一层,各层间没有反馈。是应用最广泛、发展最迅速的人工神经网络之一。
简而言之,前馈神经网络中除了全连接层 Linear 不再含有其它类型的结构,
让我们用 MegEngine 进行实现:
import megengine
import megengine.data as data
import megengine.data.transform as T
import megengine.functional as F
import megengine.module as M
import megengine.optimizer as optim
import megengine.autodiff as autodiff
def load_mnist(path, kind='train'):
import os
import gzip
import numpy as np
"""Load MNIST data from `path`"""
labels_path = os.path.join(path,
'%s-labels-idx1-ubyte.gz'
% kind)
images_path = os.path.join(path,
'%s-images-idx3-ubyte.gz'
% kind)
with gzip.open(labels_path, 'rb') as lbpath:
labels = np.frombuffer(lbpath.read(), dtype=np.uint8,
offset=8)
with gzip.open(images_path, 'rb') as imgpath:
images = np.frombuffer(imgpath.read(), dtype=np.uint8,
offset=16).reshape(len(labels), 784)
return images, labels
# Get train and test dataset and prepare dataloader
# Make sure that you have downloaded data and placed it in `DATA_PATH`
# GitHub link: https://github.com/zalandoresearch/fashion-mnist
from os.path import expanduser
DATA_PATH = expanduser("~/data/datasets/Fashion-MNIST")
X_train, y_train = load_mnist(DATA_PATH, kind='train')
X_test, y_test = load_mnist(DATA_PATH, kind='t10k')
mean, std = X_train.mean(), X_train.std()
train_dataset = data.dataset.ArrayDataset(X_train, y_train)
test_dataset = data.dataset.ArrayDataset(X_test, y_test)
train_sampler = data.RandomSampler(train_dataset, batch_size=64)
test_sampler = data.SequentialSampler(test_dataset, batch_size=64)
transform = T.Normalize(mean, std)
train_dataloader = data.DataLoader(train_dataset, train_sampler, transform)
test_dataloader = data.DataLoader(test_dataset, test_sampler, transform)
num_features = train_dataset[0][0].size
num_hidden = 256
num_classes = 10
# Define model
class NN(M.Module):
def __init__(self):
super().__init__()
self.fc = M.Linear(num_features, num_hidden)
self.classifier = M.Linear(num_hidden, num_classes)
def forward(self, x):
x = F.nn.relu(self.fc(x))
x = self.classifier(x)
return x
model = NN()
# GradManager and Optimizer setting
gm = autodiff.GradManager().attach(model.parameters())
optimizer = optim.SGD(model.parameters(), lr=0.01)
# Training and validation
nums_epoch = 5
for epoch in range(nums_epoch):
training_loss = 0
nums_train_correct, nums_train_example = 0, 0
nums_val_correct, nums_val_example = 0, 0
for step, (image, label) in enumerate(train_dataloader):
image = F.flatten(megengine.Tensor(image), 1)
label = megengine.Tensor(label).astype("int32")
with gm:
score = model(image)
loss = F.nn.cross_entropy(score, label)
gm.backward(loss)
optimizer.step().clear_grad()
training_loss += loss.item() * len(image)
pred = F.argmax(score, axis=1)
nums_train_correct += (pred == label).sum().item()
nums_train_example += len(image)
training_acc = nums_train_correct / nums_train_example
training_loss /= nums_train_example
for image, label in test_dataloader:
image = F.flatten(megengine.Tensor(image), 1)
label = megengine.Tensor(label).astype("int32")
pred = F.argmax(model(image), axis=1)
nums_val_correct += (pred == label).sum().item()
nums_val_example += len(image)
val_acc = nums_val_correct / nums_val_example
print(f"Epoch = {epoch}, "
f"train_loss = {training_loss:.3f}, "
f"train_acc = {training_acc:.3f}, "
f"val_acc = {val_acc:.3f}")
参见
本教程的对应源码: examples/beginner/neural-network.py
经过 5 轮训练,通常会得到一个正确率超过 83% (线性分类器)的神经网络模型。 在本教程中我们仅仅希望证明模型中引入非线性能具有更好的表达能力和预测性能, 因此没有花时间再去调整超参数并继续优化我们的模型。 Fashion-MNIST 数据集官方维护了一个 基准测试 结果, 可以发现其中有使用 MLPClassifier 得到的测试结果,能达到 87.7%. 我们可以根据相关模型的说明,进行模型和实验结果的复现,得到性能相当的神经网络模型。
实际上,我们从接触到神经网络模型的那一刻开始,就已经开始进入 “调参(Tuning hyperparameters)” 模式了。 神经网络模型需要正确的代码和超参数设计,才能够取得非常好的效果。 对于刚刚接触到神经网络的 MegEngine 初学者,多尝试多编码是最推荐的提升手段。 在旷视科技研究院内部将训练一个模型的过程称为 “炼丹”,如今这个词已成为行业黑话。 在完成 MegEngine 入门教程的过程中,其实就是在积累最基本的炼丹经验。
总结:再探计算图#
我们在第一篇教程中提到过计算图,现在来回忆一下:
MegEngine 是基于计算图(Computing Graph)的深度神经网络学习框架;
在深度学习领域,任何复杂的深度神经网络模型本质上都可以用一个计算图表示出来。
当我们运行本教程中的神经网络模型训练代码时,在脑海中可以去做进一步的想象,
将这个全连接神经网络表达成计算图,应该是什么样的?
我们在可视化一个神经网络模型结构时,通常关注的是数据节点的变化过程,
但计算图中的计算节点,或者说算子(Operator),也十分关键。
假定我们的算子只能为 matmul / Linear 这样的线性运算,
那么模型对输入数据的形状也会产生限制,它必须表达成一个特征向量(即 1-d 张量)。
当我们面临更加复杂的数据表征形式,比如 RGB 3 通道的彩色图片,继续使用全连接神经网络还能奏效吗?
我们在下个教程中会进行实验,接触到 CIFAR 10 彩色图片数据集,并看看全连接网络能否奏效。 届时我们会引入一种新的算子(暂时先保持神秘),发现设计神经网络其实就像搭积木一样,会有很多种不同的有效结构, 它们适用于不同的情景,而在设计算子时,一些传统领域的知识有时会很有帮助。
拓展材料#
3Blue1Brown 关于深度学习的可视化介绍视频
我们借助过可视化的形式去理解了计算机视觉中灰度图的基本表示。 可视化是我们理解数据,甚至是理解一门新知识、新概念的有效辅助手段。 我相信你已经理解了包括 “全连接神经网络(多层感知机)” 、 “梯度下降” 、“反向传播” 在内的深度学习基本概念, 而 3Blue1Brown 的视频可以作为非常好的补充:
更多 3Blue1Brown 的深度学习视频
在 Kaggle 上使用全连接神经网络刷点吧!
MNIST 和 FashionMNIST 这样的经典数据集在 Kaggle 上也有提供,你可以尝试使用 MegEngine 实现全连接神经网络模型, 尝试调整模型结构(层数、每层神经元个数)和超参数(学习率、训练轮数等等), 尽你所能地在这两个数据集上将准确率百分比点刷高,感受一下炼丹的魅力。
Kaggle 中也有许多其它人公开写好的代码,是非常不错的学习和借鉴材料。 你可能会看到一些人使用了另一种叫做 “卷积神经网络” 的模型取得了更好的效果, 这就是我们将会在下一个教程中接触到的新内容。
异或问题,人工智能的第一次寒冬
你可能在很多材料中听说过对人工智能发展历史的介绍,里面一定会提到人工智能的几次寒冬。
“感知机无法解决异或问题!” 这就是一次历史的转折点。
感知机(Perceptron)这是一种在 1950 年代末和 1960 年代初开发出的人工神经网络, 心理学家 Frank Rosenblatt 在 1957 年发布了第一个 “感知机” 模型, Marvin Minsky 和 Seymour Papert 在 1969 年出版了《感知器:计算几何导论》以作纪念。 但在这本书中对感知机做出了悲观预测,它甚至无法解决最简单的分类(异或)问题! 这导致了当时的人工智能研究方向发生了转变,导致了 1980 年代的人工智能的冬天。
尝试一下,设计出一个最简单的 XOR 神经网络模型,要求能够完全正确地得到输出。
(注:有兴趣的话,可以去了解一下人工智能的发展历史,一些纪录片和文章相当引人入胜。)
没有 Autodiff, Optimizer 和 Module 的话,将会是什么样子?
学习一个东西的最有效的办法之一是亲自去实现它(哪怕是 Naive 版本),有难度,也更花时间。
你可以尝试完全使用 NumPy 实现一个全连接神经网络(Kaggle 平台上有许多这样的例子),
不用太复杂,两层就可以了。你可以选择参考 MegEngine 中已有的设计进行实现,也可以完全自由发挥。
不要求实现自动微分系统,可以手动地将各个算子的 backward 逻辑实现出来;
也不要求利用 GPU 进行加速(毕竟需要额外学习许多知识,比如 Nvidia 的 CUDA 编程)。