Rank, Axes and Shape attributes

Note

Rank, Axes and Shape are the most basic attributes of Tensor data structure.

  • We need to pay close attention to the relationship between these three properties, they also affect our index element <access-tensor-element>specific way of.

  • If you are not very clear about the concept of these basic attributes, it will affect your understanding of How to operate Tensor.

Tensor rank

The rank of Tensor refers to the dimension of Tensor (the number of dimensions).

Warning

  • Some people also use Order and Degree to refer to the number of Tensor dimensions. At this time, the concept is equivalent to rank.

  • If you have studied linear algebra, you may have come into contact with the definition of the rank of a matrix, for example: py:func:numpy.linalg.matrix_rank. You may have seen someone use very complicated concepts to rigorously define the rank of a tensor Mathematics description… Maybe it has been confounded by different theories. But in the field of deep learning, let us keep it simple, ** rank can represent the number of dimensions of a Tensor, nothing more. **

If we say that there is a rank-2 (rank-2) Tensor, this is equivalent to the following expressions：

  • We have a matrix

  • We have a 2 dimensional array (2d-array)

  • We have a 2-dimensional tensor (2d-tensor)

Number of dimensions

However, MegEngine did not design the rank attribute for Tensor, but used the literally easier to understand: py:attr:~.Tensor.ndim, which is the abbreviation of the number of dimensions. This is also the attribute designed in NumPy to represent the number of dimensions of a multi-dimensional array: py:class:~numpy.ndarray.

>>> x = megengine.Tensor([1, 2, 3])
>>> x.ndim
1

>>> x = megengine.Tensor([[1, 2], [3, 4]])
>>> x.ndim
2

When you hear someone mention the rank of a certain Tensor, under the semantics of deep learning, you should realize that he/she refers to the dimension at this time. One possibility is that this is a user who has used the TensorFlow framework and is accustomed to using rank to describe the number of dimensions.

Okay, then we can forget the term rank and use ndim to communicate.

Note

  • In MegEngine, Tensor provides the ndim attribute to indicate the number of dimensions.

  • The value of the ``ndim’’ attribute of the Tensor corresponds to the ``n’’ in the time we often say “an n-dimensional tensor”. It tells us that we want to access a specific element from the current Tensor. The required index (Indices ). (Refer to Access an element in Tensor)

See also

For the definition of dimensionality in NumPy, please refer to: py:attr:numpy.ndarray.ndim.

Tensor axis

The dimension ndim of Tensor can lead to another related concept-Axes.

  • A one-dimensional Tensor has only one axis, and indexing its elements is like finding a specific position on a ruler whose scale is the length of the Tensor;

  • In the Cartesian plane coordinate system, there are \(X, Y\) axes. If you want to know the position of a point in the plane, you need to know the coordinate \((x, y)\).

  • Similarly, if you want to know a point in a three-dimensional space, you need to know the coordinate \((x, y, z)\), and the same is true for generalizing to higher dimensions.

Two-dimensional plane coordinate system

../../../_images/cartesian-coordinate-system.svg

via Cartesian coordinate system

Three-dimensional coordinate system

../../../_images/coord_planes_color.svg

via Three-dimensional_space

Tensor 元素索引方向 vs 空间坐标的单位向量方向

With the aid of the coordinate system, any point \(P\) in the high-dimensional space can be represented by a vector (its starting point is at the origin and the end point is at point \(P\)).

In three-dimensional space, for example, if the point :math:vector is P :math:` mathbf{r}`, Cartesian coordinates are :math:` (X, Y, Z) `, then：

\[\mathbf{r}= x {\color{red}\hat{\mathbf{i}}} + y {\color{green}\hat{\mathbf{j}}} + z {\color{blue}\hat{\mathbf{k}}}\]

The unit vector \(\hat{\mathbf{i}}, \hat{\mathbf{j}}, \hat{\mathbf{k}}\) respectively point to \(X, Y, Z\) axes. Similar to Tensor indexing specific elements, the whole process is like starting from the origin position along the axis to find the coordinates of that dimension, and then go to the next axis…

Similarly, for a high-dimensional Tensor, we can use the concept of axis to indicate the direction in which the Tensor can be manipulated in a certain dimension.

For beginners, the axis of Tensor is one of the most difficult concepts to understand, you need to understand：

The direction of the axis (Direction)

The direction of an axis represents the direction in which the index of the corresponding dimension changes.

Length of shaft (Length)

The length of an axis determines the range within which the corresponding dimension can be indexed.

The relationship between axis naming and index order

When accessing a specific element of an n-dimensional Tensor, n times of indexing are required, and each indexing is actually to find the coordinates on an axis. The naming of the axis is related to the order of the index. The first dimension to be indexed is the 0th axis ``axis=0’’, the next level is the 1st axis ``axis=1’’, and so on…

Along the axis

In some Tensor calculations, we often see that the ``axis’’ parameter needs to be specified, indicating that the calculation is along the specified axis. This means that all elements that can be obtained in the direction of the corresponding axis need to participate in the calculation.

Warning

Axes is the plural form of Axis. The former usually refers to multiple axes, and the latter usually refers to a single axis.

Let us start from the simplest case and observe the following \(M\):

\[\begin{split}M = \begin{bmatrix} 1 & 2 & 3 & 4\\ 5 & 6 & 7 & 8\\ 9 & 10 & 11 & 12\\ \end{bmatrix}\end{split}\]

When we say that this Tensor has 2 dimensions, it is equivalent to saying that this Tensor has two axes (Axes)：

  • The direction of the 0th axis ``axis=0’’ is the direction in which the row index of the matrix changes;

  • The direction of the first axis ``axis=1’’ is the direction in which the column index of the matrix changes;

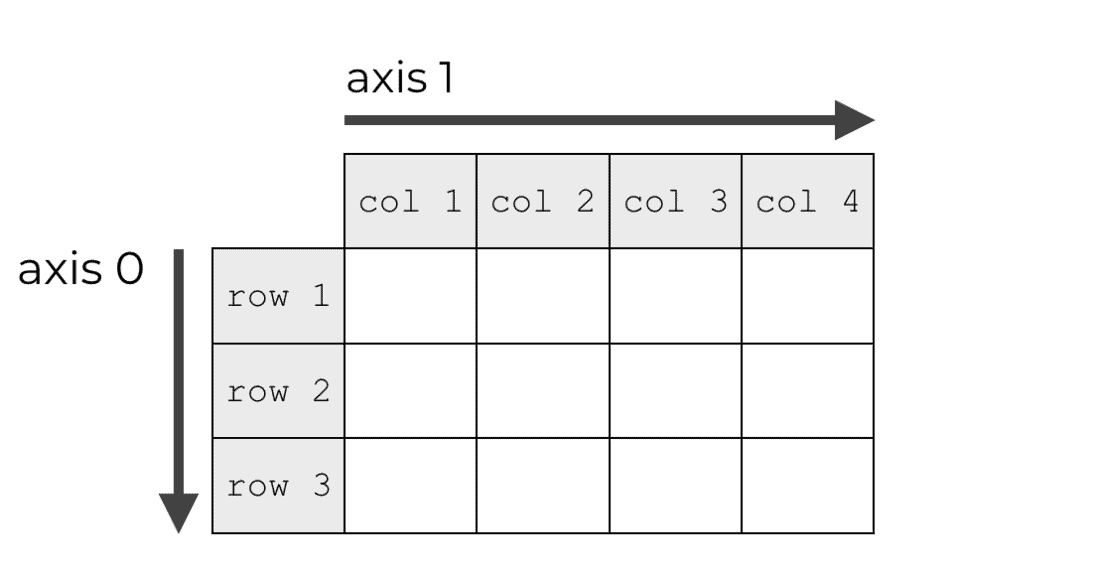
../../../_images/numpy-arrays-have-axes.png

The above picture is from an article explaining NumPy Axes (The Axes concept of NumPy multidimensional array is consistent with MegEngine Tensor).

In actual programming, the above Tensor is usually constructed like this：

>>> from megengine import tensor
>>> M = Tensor([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
>>> M.numpy()
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]], dtype=int32)

Note

The axis of a Tensor is an abstract concept, it is not a separate attribute, it is usually a parameter when operating some Tensor.

Use axis as a parameter

With the concept of axis, we can define some operations along the axis, such as sum: py:func:~.functional.sum:

Along the ``axis=0’’ direction

>>> F.sum(M, axis=0).numpy()
array([15, 18, 21, 24], dtype=int32)

Along the ``axis=1’’ direction

>>> F.sum(M, axis=1).numpy()
array([10, 26, 42], dtype=int32)

We look at what this process really happened：

Along the ``axis=0’’ direction

\[\begin{split}M = \begin{bmatrix} 1 & \color{red}{2} & \color{green}{3} & \color{blue}{4} \\ 5 & \color{red}{6} & \color{green}{7} & \color{blue}{8} \\ 9 & \color{red}{10} & \color{green}{11} & \color{blue}{12} \\ \end{bmatrix} \\ \downarrow{\text{sum()}} \\ \begin{bmatrix} 15 & \color{red}{18} & \color{green}{21} & \color{blue}{24} \end{bmatrix}\end{split}\]

Along the ``axis=1’’ direction

\[\begin{split}M = \begin{bmatrix} \color{red}1 & \color{red}2 & \color{red}3 & \color{red}4 \\ \color{green}5 & \color{green}6 & \color{green}7 & \color{green}8 \\ \color{blue}9 & \color{blue}10 & \color{blue}11 & \color{blue}12 \\ \end{bmatrix} \xrightarrow{\text{sum()}} \begin{bmatrix} \color{red}{10} \\ \ color{green}{26} \\ \color{blue}{42} \end{bmatrix}\end{split}\]

We distinguished the elements located in the same axis'' direction with colors to better understand the nature of calculation along the axis. When performing statistical calculations like ``sum() (multiple data statistics get a single statistical value), the axis parameter will control which/which axis elements are aggregated (Aggregat), Or say collapse (Collapse).

In fact, the ``ndim’’ of the returned Tensor after calculation has changed from 2 to 1.

>>> F.sum(M, axis=0).ndim
1

>>> F.sum(M, axis=1).ndim
1

See also

For more statistical calculations, please refer to: py:func:~.functional.prod, mean, min, :py: func:~.functional.max, var, std …

Note

  • This type of operation of counting the elements on a certain axis to reduce the dimensionality of the Tensor is also called Reduction.

  • Tensor splicing, expansion and other operations can also be specified on a specific axis, refer to How to operate Tensor.

Note

  • When ``ndim’’ is a 3 Tensor to operate along the axis, you can use the \(X, Y, Z\) coordinate axis in the space coordinate system to understand;

  • The operation along the axis of higher-dimensional Tensor is not easy. With visual imagination, we can understand from the perspective of element index, \(T_{[a_0][a_1]\ldots [a_{n-1}]}\) in \(i \in [0, n) \) changes.

Understand the length of the shaft

The axis of Tensor has a length, which can be understood as the number of indexes in the current dimension.

We can get the length of a Tensor on the 0th axis through the built-in Python: py:func:len. If you take out a sub-Tensor of the 0th axis and use ``len()’’ on it, you can get the sub-Tensor The length on the 0th axis corresponds to the length of the original Tensor on the 1st axis.

\[\begin{split}M_{3 \times 4} = \begin{bmatrix} \color{blue}1 & \color{blue}2 & \color{blue}3 & \color{blue}4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ \end{bmatrix} \quad M[0] = \begin{bmatrix} 1 & 2 & 3 & 4 \end{bmatrix}\end{split}\]

Take \(M\) as an example, its length on the 0th axis is 3, and its length on the 1st axis is 4.

>>> len(M)
3
>>> len(M[0])  # 取索引在 0, 1, 2 的子 Tensor 都可
4

Through ``len()’’ and index, we can always get the length of the specific axis we want to know, but this is not intuitive enough.

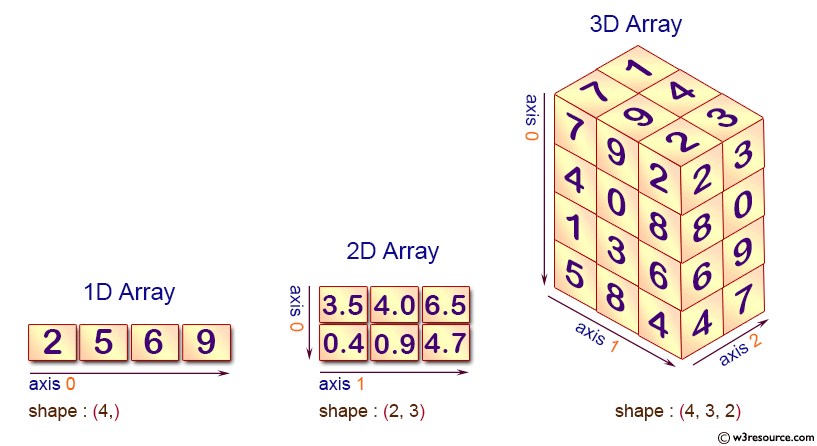
The rank of a Tensor tells us how many axes it has, and the length of each axis leads to a very important concept-Shape.

Tensor shape

Tensor has the shape: py:attr:~.Tensor.shape attribute, which is a tuple: py:class:tuple, each element in the tuple describes the length of the axis of the corresponding dimension.

>>> M.shape
(3, 4)

:math:The shape of M \((3, 4)\) tells us a lot of information：

  • \(M\) is a Tensor of rank 2, that is, a 2-dimensional Tensor, corresponding to two axes;

  • There are 3 index values available for the 0th axis and 4 index values for the 1st axis.

Tensor also has an attribute named: py:attr:~.Tensor.size, which is used to represent the number of elements in Tensor：

>>> M.size
12

We use this chart below, these relations Tensor several basic properties of intuitive display out：

../../../_images/ndim-axis-shape.png

Warning

Tensor is a zero-dimensional shape of the `` () `` need to distinguish between the difference between one-dimensional and it is only a Tensor element：

>>> a = megengine.Tensor(1)
>>> a.shape
()

>>> b = megengine.Tensor([1])
>>> b.shape
(1,)

Pay attention to the difference between “vector”, “row vector” and “column vector”：

  • A 1-dimensional Tensor is a vector, there is no difference between rows and columns in a two-dimensional space;

  • Row vector or column vector usually refers to a 2-dimensional Tensor (matrix) with a \((n,1)\) or :math:

>>> a = megengine.Tensor([2, 5, 6, 9])
>>> a.shape
(4,)

>>> a.reshape(1,-1).shape
(1, 4)

>>> a.reshape(-1,1).shape
(4, 1)

Note

  • Knowing the shape information, we can derive other basic attribute values;

  • When we perform Tensor-related calculations, we especially need to pay attention to the change of shape.

Next：more Tensor attributes

After mastering the basic properties of Tensor, we can understand How to operate Tensor, or understand Tensor element index.

The Tensor implemented in MegEngine also has more attributes, which are related to the functions supported by MegEngine——

See also

Tensor.dtype

Another attribute that a NumPy multidimensional array also has is the data type. Please refer to Tensor data type for details.

Tensor.device

Tensor can be calculated on different devices, such as GPU/CPU, etc., please refer to The device where the Tensor is located.

Tensor.grad

The gradient of Tensor is a very important attribute in neural network programming, and it is frequently used in the process of backpropagation.

The N-dimensional array ( ndarray)

Learn about the knowledge related to multi-dimensional arrays through the official NumPy documents, and compare with MegEngine’s Tensor Lenovo.

previous

Deep understanding of Tensor data structure

next

Tensor element index