How to operate Tensor

This document will show how to use the interface in functional to operate on an existing Tensor.

The similarity of these operations is that：not calculated based on the value of Tensor, and what often changes is the shape of Tensor.

Note

  • Since Tensor shape contains too much core information, we need to pay extra attention to shape changes when operating Tensor;

  • Some operations on Tensor need to be specified along the axis. If you don’t know the concept of axis, please refer to Tensor axis.

See also

  • Use: py: func: ~ .functional.copy or: py: meth:` .Tensor.to` can be obtained at the specified :ref:`resides apparatus <tensor-device>’of the Tensor;

  • Use: py: meth: .Tensor.astype Tensor can be changed to :ref:’data type <tensor-dtype>`;

  • Use: py:meth:.Tensor.item, Tensor.tolist, Tensor.numpy to convert Tensor into other data structures.

For more built-in methods, please refer to the Tensor API documentation.

Warning

The calculations in MegEngine are all performed inplace, returning a new Tensor, but the original Tensor has not changed.

>>> a = megengine.functional.arange(6)
>>> a.reshape((2, 3))
Tensor([[0. 1. 2.]
  [3. 4. 5.]], device=cpux:0)

It can be found that calling: py:meth:.Tensor.reshape will get the Tensor after ``a’’ changed shape, but ``a’’ itself has not changed：

>>> a
Tensor([0. 1. 2. 3. 4. 5.], device=cpux:0)

Warning

There is no actual data copy behind some operations. If you want to understand the underlying logic, you can refer to Tensor memory layout.

Change shape by reshaping

The feature of reshaping is that it will not change the data in the original Tensor, but will get a Tensor of a given new shape.

reshape is probably the most important operation on Tensor, suppose we now have such a Tensor:

>>> a = megengine.functional.arange(12)
>>> a
Tensor([ 0.  1.  2.  3.  4.  5.  6.  7.  8.  9. 10. 11.], device=cpux:0)
>>> a.shape
(12,)
>>> a.size
12

By: py:func:~.reshape we can change the shape without changing the size attribute:

>>> megengine.functional.reshape(a, (3, 4))
Tensor([[ 0.  1.  2.  3.]
 [ 4.  5.  6.  7.]
 [ 8.  9. 10. 11.]], device=xpux:0)

The target shape of reshape supports the existence of an axis with a value of -1, and its true value will be automatically derived from size to：

>>> a = megengine.functional.ones((2, 3, 4))
>>> a.shape
(2, 3, 4)

>>> megengine.functional.reshape(a, (-1, 4)).shape
(6, 4)

>>> megengine.functional.reshape(a, (2, -1)).shape
(2, 12)

>>> megengine.functional.reshape(a, (2, -1, 2)).shape
(2, 6, 2)

The flatten operation will flatten the sub-tensors from the start axis start_axis to the end axis end_axis, which is equivalent to a specific form of reshape:

>>> a = megengine.functional.ones((2, 3, 4))
>>> a.shape
(2, 3, 4)

>>> megengine.functional.flatten(a, 1, 2).shape
(2, 12)

And: py:func:~.transpose will change the shape according to the given template pattern：

>>> a = megengine.functional.ones((2, 3, 4))
>>> a.shape
(2, 3, 4)

>>> megengine.functional.transpose(a, (1, 2, 0)).shape
(3, 4, 2)

In the above example, the axes originally sorted as ``(0, 1, 2)’’ are changed to ``(1, 2, 0)’’ order.

See also

  • For more detailed instructions, please refer to the corresponding API documentation;

  • This type of API provides corresponding built-in method implementations in: py:class:Tensor-

    Tensor.reshape / Tensor.flatten / Tensor.transpose

Upgrading and reducing Tensor dimensionality

Another way to change the shape of a Tensor is to increase its dimensions or remove redundant dimensions. Sometimes, we use Squeeze to refer to the operation of deleting a dimension, and Unsqueeze to refer to the operation of adding a dimension. Obviously, dimensionality increase or dimensionality reduction will not change the number of elements in a Tensor, which is similar to the characteristics of reshaping Tensor.

Use: py:func:~.expand_dims to increase the dimension, you need to specify the position of the axis：

>>> a = megengine.Tensor([1, 2])
>>> b = megengine.functional.expand_dims(a, axis=0)
>>> print(b, b.shape, b.ndim)
Tensor([[1 2]], dtype=int32, device=xpux:0) (1, 2) 2

>>> b = megengine.functional.expand_dims(a, axis=1)
>>> print(b, b.shape, b.ndim)
Tensor([[1]
 [2]], dtype=int32, device=xpux:0) (2, 1) 2

As shown above, for a 1-dimensional Tensor, increase the dimension at the position of axis=0, then the elements in the original Tensor will be located at the dimension of axis=1; at the position of axis=1 Increase the dimension, and the elements in the original Tensor will be in the ``axis=0’’ dimension.

Note

Although the use of: py: func: ~ .reshape can achieve the same effect：

>>> a = megengine.Tensor([1, 2])
>>> b = megengine.functional.reshape(a, (1, -1))
>>> print(b, b.shape, b.ndim)
Tensor([[1 2]], dtype=int32, device=xpux:0) (1, 2) 2

But we should use clear semantic interfaces as much as possible.

Add a new dimension

The logic of adding dimension is very simple. The new Tensor starts from ``axis=0’’. If the dimension is obtained by: py:func:~.expand_dims, the axis length of the added dimension is 1. If this The dimension is not in the position where the new dimension needs to be added, and it is filled dimension by dimension according to the shape of the original Tensor. Examples are as follows：

>>> a = megengine.functional.ones((2, 3))
>>> b = megengine.functional.expand_dims(a, axis=1)
>>> b.shape
(2, 1, 3)

For the 2-dimensional Tensor a, we want to add a dimension at the position of axis=1. Arrange the new Tensor from axis=0''. Since ``0'' is not in the range of increasing dimensions, the ``axis=0'' dimension of the new Tensor will be performed by the 0th dimension of ``a Filling (that is, the dimension of length 2 in the example); Next, arrange the position of ``axis=1’’ in the new Tensor. This position is a new dimension, so the corresponding position axis length is 1. After adding a dimension, the original The subsequent dimensions in the Tensor (here, the dimension of length 2) will be directly connected to the current new Tensor dimension, and finally a Tensor of shape ``(2, 1, 3)’’ will be obtained.

expand_dims also supports adding multiple dimensions at once, and the rules are the same as those described above.：

>>> a = megengine.functional.ones((2, 3))
>>> b = megengine.functional.expand_dims(a, axis=(1, 2))
>>> b.shape
(2, 1, 1, 3)

>>> a = megengine.functional.ones((2, 3))
>>> b = megengine.functional.expand_dims(a, axis=(1, 3))
>>> b.shape
(2, 1, 3, 1)

Warning

Use: py:func:~.expand_dims to pay attention to the range when adding dimensions, and it should not exceed the sum of the original Tensor’s dimension ``ndim’’ and the newly added dimension：

>>> a = megengine.functional.ones((2, 3))
>>> b = megengine.functional.expand_dims(a, axis=3)
>>> b.shape
extra message: invalid axis 3 for ndim 3

In the above example, the original Tensor dimension ``ndim’’ is 2, if a new dimension is added, the final dimension of the new Tensor should be 3. The newly added axis should satisfy ``0 <= axis <= 2` `, The 3 given above has exceeded the range of dimensions that can be expressed.

Remove redundant dimensions

The opposite operation to: py:func:~.expand_dims is: py:func:~.squeeze, which can remove the dimension：

>>> a = megengine.Tensor([[1, 2]])
>>> b = megengine.functional.squeeze(a)
>>> b
Tensor([1 2], dtype=int32, device=xpux:0)

Default: py: func: ~ .squeeze remove off axis length of all of the dimension 1 may be designated by` axis` of removing：

>>> a = megengine.functional.ones((1, 2, 1, 3))
>>> megengine.functional.squeeze(a, axis=0).shape
(2, 1, 3)

>>> megengine.functional.squeeze(a, axis=2).shape
(1, 2, 3)

Similarly, squeeze supports removing multiple specified dimensions at once：

>>> megengine.functional.squeeze(a, axis=(0, 2)).shape
(2, 3)

Warning

When using squeeze to remove dimensions, pay attention to the axis length. Only redundant dimensions with an axis length of 1 can be removed.

Broadcast to Tensor

See also

See also

  • The sample graphics in this section are from the NumPy documentation, and the source code to generate them is referenced from： astroML

  • Similar APIs for expanding the shape of Tensor are：repeat / tile

The term “broadcast” describes how MegEngine handles Tensor objects with different shapes during arithmetic operations. For some reasons, the smaller Tensor needs to be broadcast based on the larger Tensor during operation, so that they have compatible shapes. The broadcast mechanism can avoid making unnecessary data copies, making the implementation of some algorithms more efficient (refer to Tensor memory layout).

Often between Tensor element-wise operation, in the simplest case, two exactly the same shape Tensor：

>>> a = megengine.Tensor([1.0, 2.0, 3.0])
>>> b = megengine.Tensor([2.0, 2.0, 2.0])
>>> a * b
Tensor([2. 4. 6.], device=xpux:0)

When the shapes of two Tensors are inconsistent, but meet the broadcast conditions, they will be broadcast to the same shape first, and then the operation will be performed.

The simplest example of a broadcast occurs in a Tensor and scalar calculation element level：

>>> a = megengine.Tensor([1.0, 2.0, 3.0])
>>> b = 2.0
>>> a * b
Tensor([2. 4. 6.], device=xpux:0)

The result is equivalent to the previous example, where b is a scalar. We can imagine that during arithmetic operations, the scalar b is stretched (Stretch) into a Tensor with the same shape as a, at this time the new element in b is just the original A copy of the scalar element. But the stretching here is just a conceptual analogy. There are some mechanisms inside MegEngine’s Tensor that can use the original scalar value uniformly without actual data copying; these mechanisms also make the broadcast behavior more memory and computational efficiency.

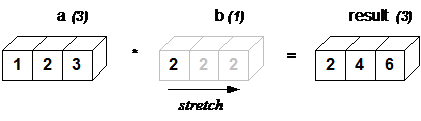
../../../_images/theory.broadcast_1.gif

In the simplest broadcast example, the scalar b is stretched into an array with the same shape as a, so these shapes are compatible with element-by-element multiplication.

We can broadcast Tensor artificially by using: py:func:~.broadcast_to, and also take b as an example：

>>> b = megengine.Tensor(2.0)
>>> broadcast_b = megengine.functional.broadcast_to(b, (1, 3))
>>> broadcast_b
Tensor([[2. 2. 2.]], device=xpux:0)

Warning

MegEngine requires: py:mod:functional API input data is Tensor, so the scalar passed to ``broadcast_to’’ here is actually a 0-dimensional Tensor. This is not the case when using ``*’’ and other arithmetic operations Therefore, there is no need to convert the input to Tensor in advance.

Broadcasting mechanism and rules

Note

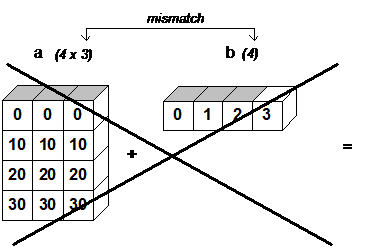
When performing operations on two Tensors, MegEngine starts from the rightmost elements of their shapes and compares them to the left one by one. When the two dimensions are compatible (meaning that the length of the corresponding axis is equal, or one of the values is 1), the corresponding operation can be performed.

If you can not meet these conditions, it will throw an exception, show shapes between the Tensor not compatible：

ValueError: operands could not be broadcast together

Warning

The broadcasting rules do not require that the tensors that are operated on have the same dimension ``ndim’’.

For example, if you have a 256 x 256 x 3 RGB value Tensor, and you want to scale each color in the image with a different value, you can multiply the image by a one-dimensional Tensor with 3 values.

Image

(3d array)

256 x

256 x

3

Scale

(1d array)

3

Result

(3d array)

256 x

256 x

3

 
>>> image = megengine.random.normal(0, 1, (256, 256, 3))
>>> scale = megengine.random.normal(0, 1, (          3,))
>>> result = image * scale
>>> print(image.shape, scale.shape, result.shape)
(256, 256, 3) (3,) (256, 256, 3)

In the following example, Tensor a and b both have axes of length 1, and these axes are expanded to a larger size in the broadcast operation.

A

(4d array)

8 x

1 x

6

1

B

(3d array)

7 x

1 x

5

Result

(4d array)

8 x

7 x

6 x

5

 
>>> a = megengine.random.normal(0, 1, (8, 1, 6, 1))
>>> b = megengine.random.normal(0, 1, (   7, 1, 5))
>>> result = a * b
>>> print(a.shape, b.shape, result.shape)
(8, 1, 6, 1) (7, 1, 5) (8, 7, 6, 5)

More broadcast visualization examples

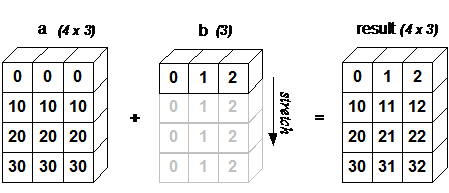
The following example shows the addition operation between two-dimensional and one-dimensional Tensor Tensor：

>>> a = megengine.Tensor([[ 0.0,  0.0,  0.0],
>>> ...                   [10.0, 10.0, 10.0],
>>> ...                   [20.0, 20.0, 20.0],
>>> ...                   [30.0, 30.0, 30.0]])
>>> b = megengine.Tensor([1.0, 2.0, 3.0])
>>> a + b
Tensor([[ 1.  2.  3.]
 [11. 12. 13.]
 [21. 22. 23.]
 [31. 32. 33.]], device=xpux:0)

As shown in the figure below, b will be added to each line of a after broadcasting.

../../../_images/theory.broadcast_2.gif

If the number of elements of the 1-dimensional Tensor matches the number of columns of the 2-dimensional Tensor, their addition will result in broadcasting.

../../../_images/theory.broadcast_3.gif

If the tail dimensions of the two Tensors are not compatible, the broadcast fails and element-level operations cannot be performed.

Splicing and segmenting Tensor

Another common type of Tensor operation is to combine multiple Tensors into one Tensor, or to split one Tensor into multiple Tensors.

concat

Connect the Tensor sequence along the existing axis.

stack

Connect the Tensor sequence along the new axis.

split

Divide the Tensor into multiple sub-Tensors of the same size.

For more interfaces and detailed instructions, please refer to Manipulation Functions API documentation.

previous

How to create a Tensor

next

How to perform scientific calculations with Tenosr