MegEngine 实现线性分类¶

本教程涉及的内容

对计算机视觉领域的图像编码有一个基础认知，了解机器学习中的分类任务；
思考线性回归模型经过什么样的变化，可用于解决分类任务，以及该采取什么样的评估指标；
根据前面的介绍，使用 MegEngine 实现线性分类器，完成 MNIST 手写数字分类任务。

可视化操作

本教程中进行了一些数据可视化操作，如果你没有 Matplotlib 的使用经验，则只需关注输出结果。

获取原始数据集¶

在上一个教程中，我们使用了 Scikit-learn 中的接口来获取加利福尼亚住房数据，并提到许多 Python 库和框架会封装好获取一些数据集的接口，方便用户调用。 MegEngine 也不例外，在 data.dataset 模块中，可以使用已经实现的数据集接口来获取原始数据集，如本次教程所需用到的 MNIST 数据集。

from megengine.data.dataset import MNIST
from os.path import expanduser

DATA_PATH = expanduser("~/data/datasets/MNIST")

train_dataset = MNIST(DATA_PATH, train=True)
test_dataset = MNIST(DATA_PATH, train=False)

和上个教程中得到的数据格式不同，这里得到的是已经划分好的训练集 train_dataset 和测试集 test_dataset, 且均已经封装成了 MegEngine 中可提供给 DataLoader 的 Dataset 类型（具体的介绍可参考使用 Dataset 定义数据集）。其中的每个元素是由单个样本 \(X_i\) 和标记 \(y_i\) 组成的元组 \((X_i, y_i)\) ：

>>> type(train_dataset[0])
tuple

为了方便进行接下来的讨论，我们这里特意地将训练数据的样本和标签拆分出来：

import numpy as np

X_train, y_train = map(np.array, train_dataset[:])

>>> print(X_train.shape, y_train.shape)
(60000, 28, 28, 1) (60000,)

统计训练样本的均值和标准差信息，用于数据预处理时进行归一化：

>>> mean, std = X_train.mean(), X_train.std()
>>> print(mean, std)
33.318421449829934 78.56748998339798

注解

对于 MNIST 这样的经典数据集，通常在数据集主页会提供这些统计信息，或可以借助搜索引擎在网络上找到其它人已经统计好的数据。

了解数据集信息¶

回忆一下，在上一个教程中，我们的住房样本数据（未拆分前）形状为 \((20640, 8)\), 表示一共有 20640 个样本，每个样本具有 8 个属性值，也可以说是特征向量的维度为 8. 而这里训练数据的形状是 \((60000, 28, 28, 1)\), 如果 60000 是训练样本的总数，那么后面的 \((28, 28, 1)\) 形状又代表什么呢？

非结构化数据：图片¶

加利福利亚住房数据集中，我们描述住房特征时可以用特征向量 \(\mathrm{x} \in \mathbb{R}^d\) 来进行表示。整个数据集可以借助二维表格（矩阵）来进行表达和存储，我们称这样的数据叫做结构化数据（Structured data）。而在现实生活中，人类更容易接触和理解的是非结构化数据（Unstructured data），比如视频、音频、图片等等…

计算机如何理解、表达和存储这样的数据呢？本教程将以 MNIST 中的手写数字图片样本为例进行说明：

>>> idx = 28204
>>> plt.title("The label is: %s" % y_train[idx])
>>> plt.imshow(X_train[idx].squeeze(), cmap="gray")
>>> plt.show()

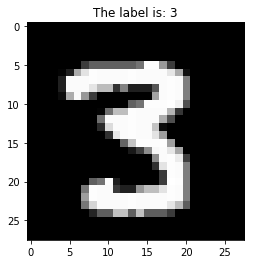
MNIST 数据集中的图像均为位图图像（Bitmap），也叫光栅图像、栅格图像，与矢量图的概念相对；每张图由许多被称作像素（Pixel, 即图像元素 Pictrue element）的点组成。我们取出一张标记为 3 的图片样本 X_train[idx] 进行观察，发现其高度（Height）和宽度（Weight）均为 28 个像素，与单个样本的形状 \((28, 28, 1)\) 对应；最后一个维度表示通道（Channel）数量，由于 MNIST 中的图片为灰度图，因此通道数为 1. 对于 RGB 颜色制式的彩图，其通道数则为 3，我们会在下一个教程中看到这样的数据。

现在让我们将这张灰度图进行 3 维可视化，以助于培养直觉理解：

>>> from mpl_toolkits.mplot3d import Axes3D
>>> ax = plt.axes(projection='3d')
>>> ax.set_zlim(-10, 255)
>>> ax.view_init(elev=45, azim=10)
>>> X, Y = np.meshgrid(np.arange(28), np.arange(28))
>>> Z = np.squeeze(X_train[idx])
>>> surf = ax.plot_surface(Y, X, Z, cmap="gray")
>>> plt.colorbar(surf, shrink=0.5, aspect=8)
>>> plt.show()

../../_images/mnist-single-example-3d.png

在灰度图中，每个像素值用 0（黑色）~ 255（白色）进行表示，即一个 int8 所能表示的范围。

我们通常称呼 \((60000, 28, 28, 1)\) 这样的数据为 NHWC 布局，在后面我们会看到更多的布局形式。

图片特征的简单处理¶

不同类型数据之间特征的区别

在上一个教程中，线性模型的单样本输入是一个特征向量 \(\mathrm{x} \in \mathbb{R}^d\);
而此处 MNSIT 数据集中的图片 \(\mathsf{I}\) 的特征空间为 \(\mathbb{R}^{H \times W \times C}\).

想要满足线性模型对输入形状的需求，需要对输入样本的特征进行一定的处理。最容易简单粗暴地实现 \(\mathbb{R}^{H \times W \times C} \mapsto \mathbb{R}^d\) 而又不丢失各元素数值信息的做法是使用 flatten 扁平化操作：

原始图像

original_image = np.linspace(0, 256, 9).reshape((3, 3))
plt.axis('off')
plt.title(f"Original Image {original_image.shape}:")
plt.imshow(original_image, cmap="gray")
plt.show()

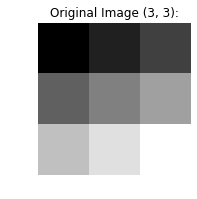
Flatten 处理后

flattened_image = original_image.flatten()
plt.axis('off')
plt.title(f"Flattened Image {flattened_image.shape}:")
plt.imshow(np.expand_dims(flattened_image, 0), cmap="gray")
plt.show()

在 MegEngine 中对应的接口为 Tensor.flatten 或 functional.flatten. 与在上个教程中提到的 expand_dims 和 squeeze 操作一样， flatten 操作也可以通过 reshape 实现。但考虑到代码语义，此时应当尽量使用 flatten 而不是 reshape.

MegEngine 中的扁平化操作可以直接用于多个样本的情况（以便支持向量化计算）：

import megengine.functional as F

x = F.ones((10, 28, 28, 1))
out = F.flatten(x, start_axis=1, end_axis=-1)

>>> print(x.shape, out.shape)
(10, 28, 28, 1) (10, 784)

经过简单处理，就能够把单个样本的线性预测模型和上一个教程中的 \(\hat{y} = \boldsymbol{w} \cdot \boldsymbol{x}+b\) 形式相互联系起来了。

分类任务的输出形式¶

在线性回归任务中，我们的预测输出值 \(\hat{y}\) 在实数域 \(\mathbb R\) 上，是连续的。而对于分类任务，通常给出的标记是由离散的值组成的集合，比如这里的 \(y \in \left\{ 0, 1, \ldots , 9 \right\}\). 此时要怎么样达成模型预测输出和标记形式上的统一呢？

让我们先简化问题的形式，从最简单的分类情况，即从二分类任务开始讨论。

二分类任务¶

假定我们的手写数字分类任务简化成标记只含有 0 和 1 的情况，即 \(y \in \left\{ 0, 1 \right\}\). 其中 0 意味着这张图片是手写数字 0, 而 1 意味着这张图片不是手写数字 0. 对于离散的标记，我们可以引入非线性的链接函数 \(g(\cdot)\) 来将线性输出映射为类别。比如，可以将 \(f(\boldsymbol{x})=\boldsymbol{x} \cdot \boldsymbol{w}+b\) 的输出以 0 为阈值（Threshold）进行划分，认为凡是计算结果大于 0 的样本，都代表这张图片是手写数字 0；而凡是计算结果小于 0 的样本，都代表这张图片不是手写数字 0. 故可以得到这样的预测模型：

\[\begin{split}\hat{y}=\mathbb{I}(f(\boldsymbol{x})-\text { threshold })= \left\{\begin{array}{lll} 1 & \text { if } & f(\boldsymbol{x})>\text { threshold } \\ 0 & \text { if } & f(\boldsymbol{x})<\text { threshold } \end{array}\right.\end{split}\]

其中 \(\mathbb I\) 是指示函数（也叫示性函数），也是我们这里用到的链接函数，但它并不常用。原因很多，对于优化问题来说，它的数学性质并不好，不适合被用于梯度下降算法。对于线性模型的输出 -100 和 -1000, 这种分段函数将二者都决策成标记为 0 的这个类别，并不能体现出两个样本类内的区别 —— 举例来说，尽管二者都不是 0，但输出为 -1000 的样本应该比输出为 -100 的样本更加不像 0. 前者可能是 1, 后者可能是 6.

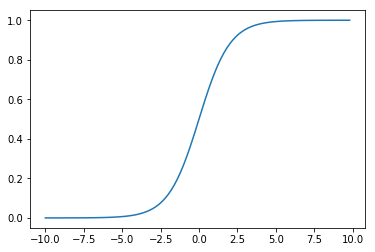
在实践中，我们更常使用的链接函数是 Sigmoid 函数 \(\sigma(\cdot)\) (也叫 Logistic 函数)：

\[\sigma(x)=\frac{1}{1+\exp (-x)}\]

def sigmoid(x):
    return 1. / (1. + np.exp(-x))

x = np.arange(-10, 10, 0.2)
y = sigmoid(x)
plt.plot(x, y)
plt.show()

其中 \(\exp\) 指以自然常数 \(e\) 为底的指数函数：

我们发现，对于二分类任务，Sigmoid 函数具有以下的优点：

易于求导：\(\sigma^{\prime}(x)=\sigma(x)(1-\sigma(x))\)
将线性计算部分的输出映射到了 \((0, 1)\) 范围内，且可以表示成概率。

我们可使用如下形式表示将样本 \(\mathrm{x}\) 的标签预测为某分类的概率（这里假定为 1）：

\[p(y=1 \mid \boldsymbol{x})=\sigma(f(\boldsymbol{x}))=\frac{1}{1+\exp (-f(\boldsymbol{x}))}\]

继续使用我们上面给出的例子：对于线性模型的输出, 经过 Sigmoid 函数的映射后， \(\sigma(-1000)\) 比 \(\sigma(-100)\) 要更加接近 0，表示前者不是 0 的概率要更高一些。这就使得不同的样本预测结果之间的区别能够得到有效的体现。与此同时，对于已经正确分类的样本，Sigmoid 函数不鼓励将线性模型的输出范围拉得过大，收益不明显。

警告

二分类 Logistic 回归最终的输出只有一个值，表示预测为某基类的概率。接下来我们将介绍多分类 Logistic 回归（Multinational Logistic Regression）。

多分类任务¶

将分类模型的输出转换为对目标类别的概率表示，是非常常见（但不唯一）的处理思路。 Logistic 回归中最终的输出只有一个概率 \(p\), 代表预测为某分类的概率；另一个分类上的概率可以直接使用 \(1-p\) 进行表示。推广到多分类任务，我们如何将线性模型的输出转换为在多个类别上的概率预测？

对标记进行 One-hot 编码

细心的读者可能已经注意到了这一点，MNIST 数据集中的标记均为标量。因此需要做一些额外的处理，使其变成多分类上的概率向量，常见的做法是使用 One-hot 编码。例如某两张手写数字样本的对应标记为 3 和 5, 使用 One-hot 编码（对应接口为 functional.nn.one_hot ）将得到如下表示：

from megengine import Tensor
import megengine.functional as F

inp = Tensor([3, 5])  # two labels
out = F.nn.one_hot(inp, num_classes=10)

>>> out.numpy()
array([[0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 1, 0, 0, 0, 0]], dtype=int32)

经过这样的处理，每个样本的标记就变成了一个 10 分类的概率向量，可与模型预测输出进行比较。

回忆一下线性回归的形式，对于单个样本 \(\boldsymbol x \in \mathbb{R}^d\), 借助于权重向量 \(\boldsymbol{w} \in \mathbb{R}^d\) 和偏置 \(b\), 可以得到一个线性输出 \(\boldsymbol {w} \cdot \boldsymbol {x} + b\), 现在我们可以将这个输出看作是预测当前样本是某个分类的得分 \(s\), 或者说预测为该分类的可信度。对于 \(c\) 分类任务，我们希望得到 \(c\) 个这样的得分，因此可以借助矩阵运算的形式实现：

\[\begin{split}\left[\begin{array}{c} -\boldsymbol{w}_{1}^{T}- \\ -\boldsymbol{w}_{2}^{T}- \\ \vdots \\ -\boldsymbol{w}_{c}^{T}- \end{array}\right] \left[\begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{d} \end{array}\right] + \left[\begin{array}{c} b_{1} \\ b_{2} \\ \vdots \\ b_{c} \end{array}\right] = \left[\begin{array}{c} \boldsymbol{w}_{1}^{T} \boldsymbol{x} + b_1 \\ \boldsymbol{w}_{2}^{T} \boldsymbol{x} + b_2 \\ \vdots \\ \boldsymbol{w}_{c}^{T} \boldsymbol{x} + b_c \end{array}\right] = \left[\begin{array}{c} s_{1} \\ s_{2} \\ \vdots \\ s_{c} \end{array}\right]\end{split}\]

注意：为了方便理解，这里写成了线性代数中矩阵运算的形式，实际计算时未必一定要将向量提升为矩阵。

我们简单验证一下输出的得分是否是一个 10 维向量（利用上一个教程中矩阵@向量运算）：

num_features = 784  # Flatten(28, 28, 1)
num_classes = 10

x = X_train[0].flatten()
W = np.zeros((num_classes, num_features))
b = np.zeros((num_classes,))
s = W @ x + b

>>> s.shape
(10,)

我们可以直观理解成，一个 \(d\) 维特征向量，经过一个权重矩阵变换加偏置后能够得到一个 \(c\) 维得分向量。

Sigmoid 函数能够将单个输出从实数域 \(\mathbb R\) 映射到概率区间 \((0,1)\) ，对于得分向量。如果每个类得分都应用 Sigmoid 函数，的确会得到多个概率值，但问题在于这样得到的概率值之和不为 1. 需要寻找其它做法。

最容易想到的做法是学习 One-hot 表示，将最大值处（对应接口 functional.argmax ）的概率设置成 1, 其它位置统统设置成 0. 如 \((10, -10, 30, 20)\) 变成 \((0, 0, 1, 0)\). \(\operatorname{Argmax}\) 这种做法属于硬分类，和之前在二分类任务中看到的示性函数 \(\mathbb I(\cdot )\) 存在着同样的问题：数学性质比较差；无法体现类内、类间样本的区别… 等等。

在多分类任务中，比较常用的是 \(\operatorname{Softmax}\) 函数（对应接口 functional.nn.softmax ）：

\[p(y=c \mid \boldsymbol{x}) =\operatorname{Softmax}\left(s_{c}\right) =\frac{\exp s_{c}}{\sum_{i} \exp s_{i}}\]

可以理解成我们对多个类上的得分经过指数归一化后得到了目标分类概率值，我们通常称为 Logits;
这种指数形式的归一化具有一些优点：相较均值归一化，具有“马太效应”，我们认为较大的原始值在归一化后得到的概率值也应该更大；顾名思义，相较于硬分类 \(\operatorname{Argmax}\) 要软（Soft）一些，可以体现类内、类间样本预测值的区别；有利于找到 Top-k 个分类候选项，即前 \(k\) 大概率的分类，有利于用作评估模型性能。

>>> score = Tensor([1, 2, 3, 4])
>>> F.softmax(score)
Tensor([0.0321 0.0871 0.2369 0.6439], device=xpux:0)

到这里，我们已经能够让我们的模型基于输入样本，输出在目标类别上进行预测的概率向量了。

分类任务的优化目标¶

我们已经得到了模型在多分类上预测的概率向量 \(\hat{\boldsymbol{y}}\), 也对真实标记通过使用 One-hot 编码得到了概率向量 \(\boldsymbol{y}\). 二者各表示一种概率分布。我们的优化目标是，让预测值和真实标记尽可能地接近，需设计合适的损失函数。

信息论中的相对熵与交叉熵

在信息论中，如果对同一个随机变量 \(x\) 有两个单独的概率分布 \(p(x)\) 和 \(q(x)\), 可以用相对熵（KL 散度）来表示两个分布之间的差异：

\[\begin{split}\begin{aligned} \mathrm{KL}(p \| q) &=-\int p(x) \ln q(x) d x-\left(-\int p(x) \ln p(x) d x\right) \\ &=H(p, q)-H(p) \end{aligned}\end{split}\]

相对熵的特点是，两个概率分布完全相同时，其值为零。二者分布之间的差异越大，相对熵值越大。

这与我们希望 “设计一个损失函数，可用来评估当前预测得到的概率分布 \(q(x)\) 与真实标记的概率分布 \(p(x)\) 之间差异” 的目的不谋而合。且由于训练过程中样本标记不会变化，其概率分布 \(p(x)\) 是确定的常数，则上式中的 \(H(p)\) 值不会随着训练样本的变化而改变，也不会影响梯度计算，所以可省略。

剩下的 \(H(p, q)\) 部分则被定义为我们常用的交叉熵（Cross Entropy, CE），用我们现在的例子中的离散概率值来表示则为：

\[\ell_{\mathrm{CE}}=H(\boldsymbol{y}, \hat{\boldsymbol{y}})=-\sum_{i=1}^{c} y_{i} \ln \hat{y}_{i}\]

这即是分类任务经常使用的损失函数，对应 MegEngine 中的 functional.nn.cross_entropy 接口。

分类任务的评估指标¶

在回归问题中常用的评估指标有 MAE, MSE 等等，但它们并不适用于分类任务。

在本教程中，我们将引入准确率（Accuracy）作为手写数字图像分类的评估指标。其定义如下：被分类正确的样本数占所有样本数的比例。例如 10000 个样本中，如果有 6000 个样本被正确分类，则我们说当前分类器的准确率为 0.6, 换算成百分比也即 60%.

对于模型预测得到的多分类上的多个输出，我们通常用 argmax 接口将最大的位置处所对应的标记作为预测分类，与真实的标记进行比较（如果是批样本的向量化实现，通常需要指定 axis 参数）：

logits = Tensor([0., 0., 0.3, 0.7, 0.,
                 0., 0., 0., 0., 0.])
pred = F.argmax(logits)

>>> pred
Tensor(3, dtype=int32, device=xpux:0)

对于在多个样本上得到的输出，我们可以借助 == 运算进行判断，以 5 个样本上预测结果为例：

>>> pred = Tensor([0, 3, 2, 4, 5])
>>> label = Tensor([0, 3, 3, 5, 2])
>>> pred == label
Tensor([ True  True False False False], dtype=bool, device=xpux:0)

这时借助 sum 接口，就能得到正确分类的样本数：

>>> (pred == label).sum().item()
2

在我们训练线性分类器的过程中，每经过一轮训练，都可以检测一下当前分类器在训练样本和测试样本上的分类准确率，作为模型性能的评估手段。如果经过多轮训练，训练集上的准确率不断上升，而测试集上的准确率开始下降，则表明可能过拟合了。

参见

准确率不是分类任务唯一的评估指标，我们会在后面的教程中接触到更多评估指标。
MegEngine 中还提供了 topk_accuracy 来计算 Top-k 准确率，而本教程中为了演示计算过程（对应 k=1 的情况），没有直接使用这个接口。

练习：线性分类器¶

结合前面提到的所有概念，现在我们使用 MegEngine 对线性分类器进行完整的实现：

可对照着上一个教程的流程进行相应环节代码的改动，体会一下整个逻辑；
再次注意，在本教程中将 MNIST 提供的测试集当做验证集进行使用（虽然名为 test ）；
对批块的数据，记得使用向量化实现来代替在单个样本上的 for 循环实现。

import megengine
import megengine.data as data
import megengine.data.transform as T
import megengine.functional as F
import megengine.optimizer as optim
import megengine.autodiff as autodiff


# Get train and test dataset and prepare dataloader
from os.path import expanduser
DATA_PATH = expanduser("~/data/datasets/MNIST")

train_dataset = data.dataset.MNIST(DATA_PATH, train=True)
test_dataset = data.dataset.MNIST(DATA_PATH, train=False)

train_sampler = data.RandomSampler(train_dataset, batch_size=64)
test_sampler = data.SequentialSampler(test_dataset, batch_size=64)

transform = T.Normalize(33.318421449829934, 78.56748998339798)

train_dataloader = data.DataLoader(train_dataset, train_sampler, transform)
test_dataloader = data.DataLoader(test_dataset, test_sampler, transform)

num_features = train_dataset[0][0].size
num_classes = 10


# Parameter initialization
W = megengine.Parameter(F.zeros((num_features, num_classes)))
b = megengine.Parameter(F.zeros((num_classes,)))


# Define linear classification model
def linear_cls(X):
    return F.matmul(X, W) + b


# GradManager and Optimizer setting
gm = autodiff.GradManager().attach([W, b])
optimizer = optim.SGD([W, b], lr=0.01)


# Training and validation
nums_epoch = 5
for epoch in range(nums_epoch):
    training_loss = 0
    nums_train_correct, nums_train_example = 0, 0
    nums_val_correct, nums_val_example = 0, 0

    for step, (image, label) in enumerate(train_dataloader):
        image = F.flatten(megengine.Tensor(image), 1)
        label = megengine.Tensor(label)

        with gm:
            score = linear_cls(image)
            loss = F.nn.cross_entropy(score, label)
            gm.backward(loss)
            optimizer.step().clear_grad()

        training_loss += loss.item() * len(image)

        pred = F.argmax(score, axis=1)
        nums_train_correct += (pred == label).sum().item()
        nums_train_example += len(image)

    training_acc = nums_train_correct / nums_train_example
    training_loss /= nums_train_example

    for image, label in test_dataloader:
        image = F.flatten(megengine.Tensor(image), 1)
        label = megengine.Tensor(label)
        pred = F.argmax(linear_cls(image), axis=1)

        nums_val_correct += (pred == label).sum().item()
        nums_val_example += len(image)

    val_acc = nums_val_correct / nums_val_example

    print(f"Epoch = {epoch}, "
          f"train_loss = {training_loss:.3f}, "
          f"train_acc = {training_acc:.3f}, "
          f"val_acc = {val_acc:.3f}")

经过 5 轮训练，通常会得到一个正确率在 92% 左右的线性分类器。

参见

本教程的对应源码： examples/beginner/linear-classification.py

总结：数据的流动¶

到目前为止，我们用线性模型完成了直线拟合、房价预测和手写数字识别任务，是时候进行一次对比了。

任务名	前向计算（单样本）	损失函数	评估指标
拟合直线	\(x \in \mathbb{R} \stackrel{w,b}{\mapsto} y \in \mathbb{R}\)	MSE	观察拟合度
房价预测	\(\boldsymbol{x} \in \mathbb{R}^{d} \stackrel{\boldsymbol{w},b}{\mapsto} y \in \mathbb{R}\)	MSE	MAE
手写数字识别	\(\boldsymbol{x} \in \mathbb{R}^{d} \stackrel{W,\boldsymbol{b}}{\mapsto} \boldsymbol{y} \in \mathbb{R}^{c}\)	CE	Accuracy

注：默认图片信息已经展平为向量，即 \(\mathsf{I} \in \mathbb{R}^{H \times W \times C} \stackrel{\operatorname{flatten}}{\mapsto} \boldsymbol{x} \in \mathbb{R}^{d}\)

在用 MegEngine 进行实现时，我们需要关注单个样本数据在整个计算图中的流动，尤其需要关注 Tensor 形状的变化（本质上这些都是线性代数中常见的变换），这其实就是我们的机器学习模型进行设计的过程，除了线性模型本身，整个机器学习流程还需要设计合适的损失函数，选定科学的评估指标。

在其它方面，几个任务的做法都是一致的，比如对于批大小的数据使用向量化实现来加速，采取的都是梯度下降算法来对模型中的参数进行迭代优化，都需要及时评估模型性能… 希望你对这些步骤已经有了更加深刻的了解。

看来线性模型就能搞定一切？

答案是否定的。由于这几个教程中数据集都过于简单，因此即使使用最简单的线性模型来训练，最终也能取得比较不错的效果。在下一个教程中，我们将选用更加复杂的数据集（相较于 MNIST 只复杂了一些些），同样是分类任务，看线性模型是否依旧那么强大。

拓展材料¶

参考文献¶

1: Yann LeCun, Corinna Cortes, and CJ Burges. Mnist handwritten digit database. ATT Labs [Online]. Available: http://yann.lecun.com/exdb/mnist, 2010.

MegEngine 实现线性回归

MegEngine 实现神经网络