Rank, Axes 与 Shape 属性#

备注

秩（Rank），轴（Axes）和形状（Shape）是 Tensor 数据结构最基本的属性。

我们需要密切关注这三个属性之间的关系，它们也会影响到我们索引元素的具体方式。
如果你对于这些基本属性的概念不是很清楚，将影响你对于如何对 Tensor 进行操作的理解。

Tensor 的秩#

Tensor 的秩（Rank）指 Tensor 的维数（维度的数量，the number of dimensions）。

警告

也有人使用阶（Order）和度（Degree）来指代 Tensor 维度的数量，此时概念等同于秩。
如果你学习过线性代数，可能接触了矩阵的秩的定义，例如 numpy.linalg.matrix_rank. 你可能也见过有人用非常复杂的概念对张量的秩进行了严谨的数学描述… 或许已被不同的说法搞得云里雾里。但是在深度学习领域，让我们保持简单，秩可以表示一个 Tensor 维度的数量，仅此而已。

如果我们说这儿有一个秩为 2 的（rank-2）Tensor，这等同于下面这些表述：

我们有一个矩阵（Matrix）
我们有一个 2 维数组（2d-array）
我们有一个 2 维张量（2d-tensor）

维度的个数#

但在 MegEngine 中并没有为 Tensor 设计 rank 这个属性，而是使用了字面上更容易理解的 ndim, 即 the number of dimensions 的缩写。这也是 NumPy 中用来表示多维数组 ndarray 维度的数量所设计的属性。

>>> x = megengine.Tensor([1, 2, 3])
>>> x.ndim
1

>>> x = megengine.Tensor([[1, 2], [3, 4]])
>>> x.ndim
2

当你听到别人提到某个 Tensor 的秩时，在深度学习的语义下，你应该意识到他/她此时指代的是维数。一种可能性是，这是一名使用过 TensorFlow 框架的用户，已经习惯了用秩来描述维度的数量。

好了，接下来我们能够忘记 rank 这种说法，用 ndim 进行交流了。

备注

在 MegEngine 中为 Tensor 提供了 ndim 属性，用来表示维度的数量。
Tensor 的 ndim 属性的值对应我们常说的 “一个 n 维张量” 时中的 n. 它告诉我们想要从当前这个 Tensor 中访问特定元素时所需索引（Indices）的个数。（参考访问 Tensor 中某个元素）

参见

NumPy 中对于维数的定义请参考 numpy.ndarray.ndim.

Tensor 的轴#

Tensor 的维数 ndim 可以引出另一个相关的概念——轴（Axes）。

一维 Tensor 只有一个轴，索引其中的元素就好像在刻度为单位 Tensor 长度的尺子上找到特定的位置；
在笛卡尔平面坐标系中，存在着 \(X, Y\) 轴，想要知道平面中某个点的位置，就需要知道坐标 \((x, y)\).
同样地，想要知道三维空间中的一个点，就需要知道坐标 \((x, y, z)\), 推广到更高维也是如此。

二维平面坐标系

../../../_images/cartesian-coordinate-system.svg — via Cartesian coordinate system#

三维空间坐标系

../../../_images/coord_planes_color.svg — via Three-dimensional_space#

同样地，对于一个高维 Tensor, 我们可以借助轴的概念，用来表明 Tensor 某个维度可操作的方向。

对初学者来说，Tensor 的轴是最难理解的概念之一，你需要明白：

轴的方向（Direction）

一个轴的方向代表对应维度的索引进行变化的方向。

轴的长度（Length）

一个轴的长度决定对应维度能够进行索引的范围。

轴的命名与索引顺序的关系

在访问 n 维 Tensor 的特定某个元素时，需要进行 n 次索引，每次索引其实就是在一个轴上找坐标。轴的命名与索引的顺序有关，首先被索引的维度是第 0 轴 axis=0, 往内一层是第 1 轴 axis=1, 依此类推…

沿着轴（Along the axis）

在一些 Tensor 计算中，我们经常会看到需要指定 axis 参数，表明沿着指定轴计算。这意味着在对应轴的方向上所能取得的所有元素都需要参与计算。

警告

Axes 是 Axis 的复数形式，前者通常指代多个轴，后者通常指代单条轴。

让我们从最简单的情况开始，观察下面这个由矩阵（2 维数组） \(M\) 表示的 Tensor:

\[\begin{split}M = \begin{bmatrix} 1 & 2 & 3 & 4\\ 5 & 6 & 7 & 8\\ 9 & 10 & 11 & 12\\ \end{bmatrix}\end{split}\]

当我们说这个 Tensor 有 2 个维度时，等价于在说这个 Tensor 有两个轴（Axes）：

第 0 轴 axis=0 的方向即矩阵的行（Row）索引变化的方向；
第 1 轴 axis=1 的方向即矩阵的列（Column）索引变化的方向；

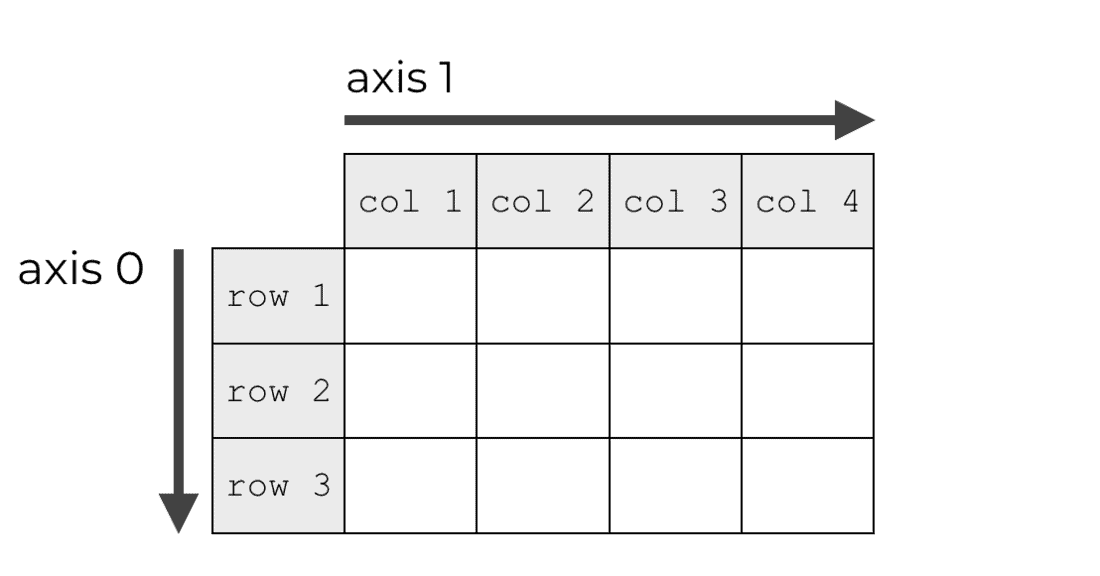
../../../_images/numpy-arrays-have-axes.png

上图来自于一篇解释 NumPy Axes 的文章（NumPy 多维数组的 Axes 概念与 MegEngine Tensor 一致）。

实际编程时，上面这个 Tensor 通常是这样构造的：

>>> from megengine import tensor
>>> M = Tensor([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
>>> M.numpy()
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]], dtype=int32)

备注

Tensor 的轴是一个抽象的概念，它不是一个单独的属性，通常是操作某些 Tensor 时的参数。

使用 axis 作为参数#

有了轴的概念，我们便可以定义一些沿着轴的操作，比如求和 sum :

沿着 axis=0 方向

>>> F.sum(M, axis=0).numpy()
array([15, 18, 21, 24], dtype=int32)

沿着 axis=1 方向

>>> F.sum(M, axis=1).numpy()
array([10, 26, 42], dtype=int32)

我们看看这个过程中究竟发生了什么：

沿着 axis=0 方向

\[\begin{split}M = \begin{bmatrix} 1 & \color{red}{2} & \color{green}{3} & \color{blue}{4} \\ 5 & \color{red}{6} & \color{green}{7} & \color{blue}{8} \\ 9 & \color{red}{10} & \color{green}{11} & \color{blue}{12} \\ \end{bmatrix} \\ \downarrow{\text{sum()}} \\ \begin{bmatrix} 15 & \color{red}{18} & \color{green}{21} & \color{blue}{24} \end{bmatrix}\end{split}\]

沿着 axis=1 方向

\[\begin{split}M = \begin{bmatrix} \color{red}1 & \color{red}2 & \color{red}3 & \color{red}4 \\ \color{green}5 & \color{green}6 & \color{green}7 & \color{green}8 \\ \color{blue}9 & \color{blue}10 & \color{blue}11 & \color{blue}12 \\ \end{bmatrix} \xrightarrow{\text{sum()}} \begin{bmatrix} \color{red}{10} \\ \color{green}{26} \\ \color{blue}{42} \end{bmatrix}\end{split}\]

我们将位于同一个 axis 方向上的元素用颜色进行了区分，来更好地理解沿着轴计算的本质。在进行类似 sum() 这样的统计性质的计算（多个数据统计得到单个统计值）时， axis 参数将控制对哪个/哪些轴上的元素进行聚合（Aggregat），或者说折叠（Collapse）。

实际上，计算后的返回的 Tensor 的 ndim 已经由 2 变成了 1.

>>> F.sum(M, axis=0).ndim
1

>>> F.sum(M, axis=1).ndim
1

参见

更多统计性质的计算请参考 prod, mean, min, max, var, std …

备注

这种对某个轴上的元素进行统计，使得 Tensor 维数减少的操作也叫做归约运算（Reduction）。
Tensor 的拼接、拓展等操作也可以指定在特定的轴上进行，参考如何对 Tensor 进行操作。

备注

ndim 为 3 的 Tensor 进行沿轴操作时，可以借助空间坐标系中存在的 \(X, Y, Z\) 坐标轴理解；
更高维 Tensor 的沿轴操作不好借助视觉想象，我们可以通过元素索引的角度来理解， \(T_{[a_0][a_1]\ldots [a_{n-1}]}\) 中的 \(i \in [0, n)\) 轴方向即对应索引 \(a_i\) 变化的方向。

理解轴的长度#

Tensor 的轴具有长度，可以理解成当前维度的索引个数。

我们可以通过 Python 内置的 len 来获取一个 Tensor 在第 0 轴的长度，如果取出第 0 轴的某个子 Tensor, 对它使用 len() 则可以获得子 Tensor 在第 0 轴的长度，对应于原 Tensor 在第 1 轴的长度。

\[\begin{split}M_{3 \times 4} = \begin{bmatrix} \color{blue}1 & \color{blue}2 & \color{blue}3 & \color{blue}4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ \end{bmatrix} \quad M[0] = \begin{bmatrix} 1 & 2 & 3 & 4 \end{bmatrix}\end{split}\]

以 \(M\) 为例，它在第 0 轴的长度为 3, 在第 1 轴的长度为 4.

>>> len(M)
3
>>> len(M[0])  # 取索引在 0, 1, 2 的子 Tensor 都可
4

通过 len() 和索引，我们总是能获得想要知道的特定轴的长度，但这样不够直观。

Tensor 的秩告诉我们它具有多少个轴，而每个轴的长度引出了一个非常重要的概念——形状（Shape）。

Tensor 的形状#

Tensor 具有形状 shape 属性，它是一个元组 tuple, 元组中的每个元素描述了对应维度的轴的长度。

>>> M.shape
(3, 4)

\(M\) 的形状 \((3, 4)\) 告诉我们非常多的信息：

\(M\) 是一个秩为 2 的 Tensor, 也即 2 维 Tensor, 对应有两个轴；
第 0 轴有 3 个索引值可用，第 1 轴有 4 个索引值可用。

Tensor 还具备名为 size 的属性，用来表示 Tensor 中元素的个数：

>>> M.size
12

我们借助下面这张图，将这几个 Tensor 基础属性的关系直观地展示出来：

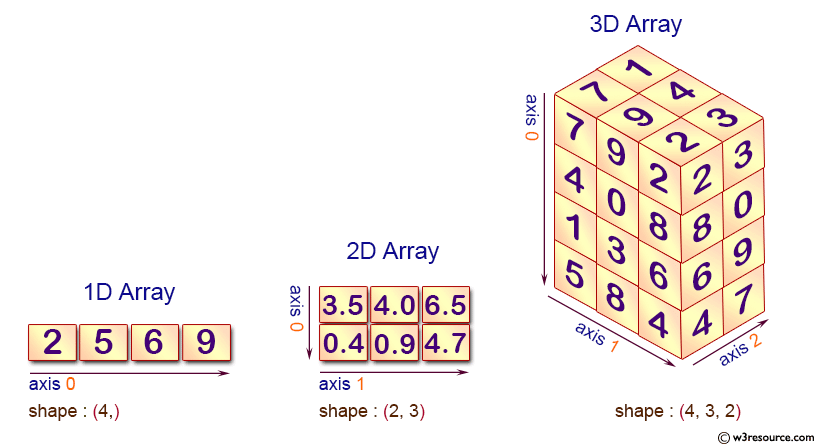
警告

0 维 Tensor 的形状为 (), 需要区分它和只有一个元素的 1 维 Tensor 的区别：

>>> a = megengine.Tensor(1)
>>> a.shape
()

>>> b = megengine.Tensor([1])
>>> b.shape
(1,)

注意 “向量”、“行向量”、“列向量” 的区别：

1 维 Tensor 是一个向量，没有二维空间中行与列的区别；
行向量或列向量通常指形状为 \((n,1)\) 或 \((1,n)\) 的 2 维 Tensor（矩阵）

>>> a = megengine.Tensor([2, 5, 6, 9])
>>> a.shape
(4,)

>>> a.reshape(1,-1).shape
(1, 4)

>>> a.reshape(-1,1).shape
(4, 1)

备注

知道了形状信息，我们就可以推导出其它基础的属性值；
我们在进行 Tensor 有关的计算时，尤其需要关注形状的变化。

接下来：更多的 Tensor 属性#

掌握 Tensor 的基本属性后，我们便可以了解如何对 Tensor 进行操作，或者了解 Tensor 元素索引。

MegEngine 中实现的 Tensor 还具备有更多的属性，它们与 MegEngine 所支持的功能有关 ——

参见

Tensor.dtype: 另外一个 NumPy 多维数组也具备的属性是数据类型，请参考 Tensor 数据类型了解细节。
Tensor.device: Tensor 可以在不同的设备上进行计算，比如 GPU/CPU 等，请参考 Tensor 所在设备。
Tensor.grad: Tensor 的梯度是神经网络编程中很重要的一个属性，在反向传播的过程中被频繁使用。
The N-dimensional array ( ndarray ): 通过 NumPy 官方文档了解与多维数组有关的知识，与 MegEngine 的 Tensor 联想对比。