使用 Module 构造模型结构

在 MegStudio 运行	查看源文件

在本次教程中，你将会学习到在实际开发中我们更加常用的 Module 建模方式与工程化技巧，通过实现几个比 LeNet 更复杂的经典 CNN 模型结构，感受一下其优点。

• 我们将尝试使用面向对象的思想，通过自定义 Module 类来构建 LeNet 模型，并灵活地取得内部结构信息，同时完成对 Parameters 的相关处理；

• 我们将接触到 AlexNet, VGGNet 和 GoogLeNet 三种经典的模型结构，并学会一些实用的编码技巧；

• 我们还将了解到如何保存和加载我们的模型，有利于在不同的设备上进行训练和迁移；

• 与此同时，我们的代码将逐渐变得工程化，这有利于将来我们写出可读性、可维护性更好的代码，也方便我们阅读其它开源的模型代码文件。

与之前的教程不同，这次的教程需要你 花费更多的时间去理解不同的代码 ，将抽象的概念变为具体的代码实践。

请先运行下面的代码，检验你的环境中是否已经安装好 MegEngine（安装教程）：

import megengine

print(megengine.__version__)

import numpy as np
import megengine.autodiff as autodiff
import megengine.data as data
import megengine.data.transform as T
import megengine.functional as F
import megengine.optimizer as optim

1.5.0

神经网络中的模块（Module）

在神经网络模型中，经常存在着许多非常相似的结构，比如全连接的前馈神经网络中，每个层都是线性层。而在卷积神经网络中，卷积层、池化层也非常常见。

• 与 add(), sub()… 等通用的 functional 算子不同，网络层结构中通常存在着需要被管理的参数 Parameter, 包括初始化和更新等操作；

• 我们此前一直关注于“单个”的概念，即计算图中的“单个”计算节点/数据节点，神经网络中“单个”神经元/层… 现在我们需要想一想复杂规模下的情景；

• 当模型结构变得越来越复杂，如果依旧通过枚举的方式来初始化和绑定参数，依靠 funtional API 写出完整的结构，代码非常不优雅，且和工程化的理念不符；

我们构建神经网络所需的主要组件是层（Layer），最好能够提供一种足够的抽象机制，方便用户进行模型定义和参数管理，复用相似的结构。

为此，MegEngine 拓展出了 Module 类，这意味着我们需要使用到一些面向对象编程（OOP）的思想。

Module 类实现在 megengine.module 子包中，让我们先进行导入，并且使用 M 作为别名：

import megengine.module as M

print(type(M.Module))

<class 'abc.ABCMeta'>

• Module 类是所有的神经网络层的基类，我们提到 Module 类时，通常指代的是这个基类；

• Module 类本身是一个抽象类，在我们定义的模型中无法被直接使用；

• MegEngine 中实现的所有层都继承了 Module 基类中的内置方法，并且对其进行了相应的拓展；

我们需要建立这样一个观念，一个神经网络模型可以由多个小的层（Layer）级别的 Module 构成，与此同时它的子结构（甚至是它本身）也可以被视作是一个大的 Module.

这种感觉有点类似于玩乐高积木，最基础的积木块总是定义好的，但我们总是可以参照着一些模版拼出更加复杂的结构，这个结构本身也可以作为更大结构的一部分，而你是设计蓝图的工程师。

积木从哪儿来呢？除了 Module 基类，我们可以在 megengine.module 子包中找到更多常见层的实现：

• 与 functional.conv2d 对应的层是 module.Conv2d;

• 与 functional.linear 对应的层是 module.Linear;

• 可以发现二者命名十分相似，通常我们总是能够在 module 中找到与 funtional 对应的算子。

接下来我们需要做的是搭积木，在自定义我们的神经网络模型时，需要注意以下细节：

• 每一个神经网络模型都需要继承自 Module 基类并且调用super().__init__();

• 我们需要在 __init__ 构造函数中定义模块结构，也可以做一些其它初始化处理（后面会看到）；

• 我们需要定义 forward 方法，在里面实现前向传播的计算过程；

• 显然，由于 MegEngine 中实现了自动求导机制，我们不需要对 backward() 方法进行实现。

我们现在就来改写 LeNet 模型，这样能对刚才提到的概念有一个更加直观的理解：

class LeNet(M.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = M.Conv2d(3, 6, 5)
        self.conv2 = M.Conv2d(6, 16, 5)
        self.fc1   = M.Linear(16*5*5, 120)
        self.fc2   = M.Linear(120, 84)
        self.fc3   = M.Linear(84, 10)

    def forward(self, x):
        x = F.max_pool2d(F.relu(self.conv1(x)), 2)
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = F.flatten(x, 1)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

在 LeNet 内部发生了什么呢？目前我们需要知道：

• LeNet 模型内部的每一层（如 conv1）也是一个 Module, 在它们的内部各自封装好了 forward 实现和需要用到的参数；

• 每层的参数可以随着 LeNet 模型在训练过程中学习而更新，这也是我们将这些层指定为 LeNet 类内属性的原因。

lenet = LeNet()
print(lenet)

LeNet(
  (conv1): Conv2d(3, 6, kernel_size=(5, 5))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

我们可以对 LeNet 中的子 Module 成员进行修改替换，但这是比较进阶的处理方式，目前我们只需对此保有概念即可。

使用 Sequential 顺序容器

在 MegEngine 中也提供了 Module 的有序容器 Sequential, 一种用法如下：

mini_net =  M.Sequential(
    M.Linear(1, 1),
    M.Linear(1, 1)
)
print(mini_net)

mini_data = megengine.Parameter([[1]])
output = mini_net(mini_data)
print(output)

Sequential(
  (0): Linear(in_features=1, out_features=1, bias=True)
  (1): Linear(in_features=1, out_features=1, bias=True)
)
Tensor([[-0.0985]], device=xpux:0)

你应该发现了，我们可以直接使用 Sequential 定义的模型处理数据，而无需在内部指定 forward() 流程，因为在序列定义时即决定了前向传播的顺序。

接下来我们用 Sequential 组合来实现 LeNet 模型：

• 由于是 Module 容器，对内部元素类型有要求，因此 relu 等算子也存在着 ReLU 这样的 Module 实现；

• 默认情况下，Sequential 将以 \(0, 1, 2, 3, \ldots\) 顺序对内部的 Module 进行命名；

• 注意我们这里的代码有些不一样，我们将模型整理了 features 和 classifier 两个部分，

class SequentialLeNet(M.Module):
    def __init__(self):
        super().__init__()
        self.features = M.Sequential(
            M.Conv2d(3, 6, 5),
            M.ReLU(),
            M.MaxPool2d(2),
            M.Conv2d(6, 16, 5),
            M.ReLU(),
            M.MaxPool2d(2)
        )
        self.classifer = M.Sequential(
            M.Linear(16*5*5, 120),
            M.ReLU(),
            M.Linear(120, 84),
            M.ReLU(),
            M.Linear(84, 10)
        )

    def forward(self, x):
        x = self.features(x)
        x = F.flatten(x, 1)
        x = self.classifer(x)
        return x

squential_lenet = SequentialLeNet()
print(squential_lenet)

SequentialLeNet(
  (features): Sequential(
    (0): Conv2d(3, 6, kernel_size=(5, 5))
    (1): ReLU()
    (2): MaxPool2d(kernel_size=2, stride=2, padding=0)
    (3): Conv2d(6, 16, kernel_size=(5, 5))
    (4): ReLU()
    (5): MaxPool2d(kernel_size=2, stride=2, padding=0)
  )
  (classifer): Sequential(
    (0): Linear(in_features=400, out_features=120, bias=True)
    (1): ReLU()
    (2): Linear(in_features=120, out_features=84, bias=True)
    (3): ReLU()
    (4): Linear(in_features=84, out_features=10, bias=True)
  )
)

另一种用法是使用 OrderedDict 定义，这样内部的 Module 可具有指定的名字：

from typing import OrderedDict

class NamedSequentialLeNet(M.Module):
    def __init__(self):
        super().__init__()
        self.features = M.Sequential(OrderedDict([
            ('conv1', M.Conv2d(3, 6, 5)),
            ('relu1', M.ReLU()),
            ('max_pool1', M.MaxPool2d(2)),
            ('conv2', M.Conv2d(6, 16, 5)),
            ('relu2', M.ReLU()),
            ('max_pool2', M.MaxPool2d(2))
        ]))
        self.classifer = M.Sequential(OrderedDict([
            ('fc1', M.Linear(16*5*5, 120)),
            ('relu3', M.ReLU()),
            ('fc2', M.Linear(120, 84)),
            ('relu4', M.ReLU()),
            ('fc3', M.Linear(84, 10))
        ]))

    def forward(self, x):
        x = self.features(x)
        x = F.flatten(x, 1)
        x = self.classifer(x)
        return x

named_squential_lenet = NamedSequentialLeNet()
print(named_squential_lenet)

NamedSequentialLeNet(
  (features): Sequential(
    (conv1): Conv2d(3, 6, kernel_size=(5, 5))
    (relu1): ReLU()
    (max_pool1): MaxPool2d(kernel_size=2, stride=2, padding=0)
    (conv2): Conv2d(6, 16, kernel_size=(5, 5))
    (relu2): ReLU()
    (max_pool2): MaxPool2d(kernel_size=2, stride=2, padding=0)
  )
  (classifer): Sequential(
    (fc1): Linear(in_features=400, out_features=120, bias=True)
    (relu3): ReLU()
    (fc2): Linear(in_features=120, out_features=84, bias=True)
    (relu4): ReLU()
    (fc3): Linear(in_features=84, out_features=10, bias=True)
  )
)

Sequential 除了本身可以用来定义模型之外，它还可以用来快速包装可被复用的模型结构，我们在 VGG 等模型中会见到更加高级的用法。

Module 内置方法

光看上面提到的用法，似乎感受不到太多 module 实现模型结构相较于 funtional 的优势。

接下来才是重头戏，我们将介绍 Module 类中经常被使用到的方法：

• modules(): 返回一个可迭代对象，可以遍历当前模块中的所有模块，包括其本身;

• named_modules(): 返回一个可迭代对象，可以遍历当前模块包括自身在内的 key 与 Module 键值对，其中 key 是从当前模块到各子模块的点路径。

• parameters(): 返回一个可迭代对象，遍历当前模块中的所有 Parameter;

• named_parameters(): 返回一个可迭代对象，可以遍历当前模块中 key 与 Parameter 组成的键值对。其中 key 是从模块到 Parameter 的点路径。

• state_dict(): 返回一个有序字典，其键值对是每个网络层和其对应的参数。

Module 可以直接作为 Python List 或者 Dict 等数据结构中的元素进行组合使用，一个父 Module 会自动地将子 Module 中存在的 Parameter 进行注册。

除此以外还提供了 buffers(), children() 等方法，通过在文档中搜索和阅读 Module API, 可以了解更多细节。

modules() 与 named_modules()

我们首先看一下使用 module 方式实现的 LeNet 结构中存在着哪些模块：

for name, module in lenet.named_modules():
    print(name, module)

 LeNet(
  (conv1): Conv2d(3, 6, kernel_size=(5, 5))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)
conv1 Conv2d(3, 6, kernel_size=(5, 5))
conv2 Conv2d(6, 16, kernel_size=(5, 5))
fc1 Linear(in_features=400, out_features=120, bias=True)
fc2 Linear(in_features=120, out_features=84, bias=True)
fc3 Linear(in_features=84, out_features=10, bias=True)

parameters() 与 named_parameters（）

接下来我们需要关注一下模型中的参数（具体来说是权重 weight 和偏置 bias）：

for name, parameter in lenet.named_parameters():
    print(name, parameter.shape, type(parameter))

conv1.bias (1, 6, 1, 1) <class 'megengine.tensor.Parameter'>
conv1.weight (6, 3, 5, 5) <class 'megengine.tensor.Parameter'>
conv2.bias (1, 16, 1, 1) <class 'megengine.tensor.Parameter'>
conv2.weight (16, 6, 5, 5) <class 'megengine.tensor.Parameter'>
fc1.bias (120,) <class 'megengine.tensor.Parameter'>
fc1.weight (120, 400) <class 'megengine.tensor.Parameter'>
fc2.bias (84,) <class 'megengine.tensor.Parameter'>
fc2.weight (84, 120) <class 'megengine.tensor.Parameter'>
fc3.bias (10,) <class 'megengine.tensor.Parameter'>
fc3.weight (10, 84) <class 'megengine.tensor.Parameter'>

这意味着，我们既可以借助 parameters() 完成整体性的操作，也可以根据 name 进行精细化的处理。

比如，我们可以通过添加一些 if 逻辑来对满足规则的参数进行操作（作为演示，下面的代码中仅做了 print 操作）：

for name, parameter in lenet.named_parameters():
    if "conv" in name:
        print(name, parameter.shape)

conv1.bias (1, 6, 1, 1)
conv1.weight (6, 3, 5, 5)
conv2.bias (1, 16, 1, 1)
conv2.weight (16, 6, 5, 5)

更常见的使用情景是，我们可以在定义求导器和优化器时，非常方便地对所有参数进行绑定：

gm = autodiff.GradManager().attach(lenet.parameters())
optimizer = optim.SGD(lenet.parameters(), lr=1e-3)

使用 state_dict() 获取信息

调用 Module.state_dict() 将返回一个有序字典，因此我们可以先看看内部的键有什么：

print(lenet.state_dict().keys())
print(lenet.conv1.state_dict().keys())

odict_keys(['conv1.bias', 'conv1.weight', 'conv2.bias', 'conv2.weight', 'fc1.bias', 'fc1.weight', 'fc2.bias', 'fc2.weight', 'fc3.bias', 'fc3.weight'])
odict_keys(['bias', 'weight'])

很自然地，我们可以通过 state_dict()['name'] 的形式来获取某一层的参数信息：

print(lenet.state_dict()['conv1.weight'].shape)
print(lenet.conv1.state_dict()['weight'].shape) # 这种写法也是可以的

(6, 3, 5, 5)
(6, 3, 5, 5)

我们也可以通过使用 named_parameters() 来取得同样的效果，但显然这样做比较麻烦，效率也比较低：

# 将 generator 变成 list
params = list(lenet.named_parameters())
print("To list:", params[1][1].shape)

# 将 generator 变成 dict
params = {}
for name, param in lenet.named_parameters():
    params[name] = param
print("To dict:", params['conv1.weight'].shape)

To list: (6, 3, 5, 5)
To dict: (6, 3, 5, 5)

另外，在 Optimizer 中也提供了 state_dict() 方法，可以用来获取学习率等超参数信息，这在需要保存和加载状态信息时能派上用场。

如何实现共享参数

有时候我们需要对模型的相同结构部分参数进行共享，实现起来也很简单：

• 由于 Parameters 其实就是一个 Tensor 的子类，如果要共享某一层的参数，只需要在 Module 类的 forward() 函数里多次调用这个层；

• 使用 Sequantial 多次传入同一个 Module 对象，也可以实现参数的共享（我们这里没有进行举例）。

# 在 forward 方法中重复调用同一个层
class SharedNet(M.Module):
    def __init__(self):
        super().__init__()
        self.linear = M.Linear(1, 1)

    def forward(self, x):
        x = self.linear(x)
        x = self.linear(x)
        x = self.linear(x)
        x = self.linear(x)
        return x

shared_net = SharedNet()
print(shared_net) # 将显示出只有一个 linear 层

SharedNet(
  (linear): Linear(in_features=1, out_features=1, bias=True)
)

x = megengine.Parameter([[1]])

# 将 parameter 初始化为 3, 共享同一层，所以 "Init" 只输出了两次，对应 0.weight 和 0.bias
for name, parameter in shared_net.named_parameters():
    M.init.fill_(parameter, 3) # 我们即将介绍这句代码的作用
    print("Inited", name, parameter)

gm = autodiff.GradManager().attach(shared_net.parameters())
optimizer = optim.SGD(shared_net.parameters(), lr=0.01)

with gm:
    y = shared_net(x)
    gm.backward(y)
optimizer.step()
optimizer.clear_grad()

print(y) # (((1 * 3 + 3) * 3 + 3) * 3 + 3) * 3 + 3 = 201

Inited linear.bias Parameter([3.], device=xpux:0)
Inited linear.weight Parameter([[3.]], device=xpux:0)
Tensor([[201.]], device=xpux:0)

可以发现，对于 shared_net 和 sequential_shared_net, 虽然实际进行了四次线性层运算，但显示出的模型结构却只有一层，表明参数进行了共享。

现在请你思考一下，对于共享的参数，反向传播的更新策略是什么样的呢？（你可以通过编码验证自己的想法）

对于一些进阶的参数处理情景（比如训练过程中对学习率的更改、固定部分参数不优化等等），可以参考 MegEngine 用户指南。

Module 参数初始化

敏锐的你或许已经注意到了：我们在上面进行了 Module 参数的初始化操作，接下来我们将介绍为此而设计的 init 子模块。

在 module 模块中，实现了 init 子模块，即初始化（Initialization）模块，里面包含着常见的初始化方式：

• init.zeros_(): 0 值初始化

• init.ones_(): 1 值初始化

• init.fill_(): 根据给定值进行初始化

weight = megengine.Parameter([1, 2, 3])

M.init.zeros_(weight)
print(weight)

M.init.ones_(weight)
print(weight)

M.init.fill_(weight, 6)
print(weight)

Parameter([0 0 0], dtype=int32, device=xpux:0)
Parameter([1 1 1], dtype=int32, device=xpux:0)
Parameter([6 6 6], dtype=int32, device=xpux:0)

除此以外还实现了一些统计学意义上的随机初始化策略，如 init.uniform_(), init.normal_ 等。

我们在这里不进行过多的说明，你可以通过查看 Module.init API 文档以了解更多细节。

默认初始化策略

我们曾经提到，神经网络模型的参数使用全零初始化不是一个好策略，只是目前我们还没有解释原因。

常见 Module 的基类实现中会有一个默认的参数初始化策略：

• 比如 Conv1d 和 Conv2d 其实都继承自 _ConvNd, 而在 _ConvNd 的 __init__() 方法中进行了参数初始化；

• 阅读下面的部分源代码，你会发现 Linear 也采用了与 _ConvNd 类似的默认初始化策略；

# path: megengine/module/conv.py

class _ConvNd(Module):
    def __init__(...):
        #...
        self.reset_parameters()

    @abstractmethod
    def _get_fanin(self):
        pass

    def reset_parameters(self) -> None:
        fanin = self._get_fanin()
        std = np.sqrt(1 / fanin)
        init.normal_(self.weight, 0.0, std)
        if self.bias is not None:
            init.zeros_(self.bias)

    #...


class Conv2d(_ConvNd):

    #...

    def _get_fanin(self):
        kh, kw = self.kernel_size
        ic = self.in_channels
        return kh * kw * ic

# path: megengine/module/linear.py

class Linear(Module):

    def __init__(self, in_features: int, out_features: int, bias: bool = True, **kwargs):
        #...
        self.reset_parameters()

    def _get_fanin(self):
        return self.in_features

    def reset_parameters(self) -> None:
        fanin = self._get_fanin()
        std = np.sqrt(1 / fanin)
        init.normal_(self.weight, 0.0, std)
        if self.bias is not None:
            init.zeros_(self.bias)

阅读源代码是我们了解程序本质的好方法——源码面前，了无秘密。

通过阅读 MegEngine 的源代码，能帮助我们更好地使用该框架，甚至拓展开发出自己想要的功能，这不失为一种提升自己的方式。

自定义初始化策略

在实际的模型设计中，默认的初始化策略可能无法满足需求，因此总会有需要自己定义初始化策略的时候。

我们重新定义一个 CustomInitLeNet 类，并且在里面完成自定义初始化策略的设置：

import math

class CustomInitLeNet(M.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = M.Conv2d(3, 6, 5)
        self.conv2 = M.Conv2d(6, 16, 5)
        self.fc1   = M.Linear(16*5*5, 120)
        self.fc2   = M.Linear(120, 84)
        self.fc3   = M.Linear(84, 10)

        # 自定义的初始化策略，覆盖掉默认的处理方式
        for m in self.modules():
            if isinstance(m, M.Conv2d):
                M.init.msra_normal_(m.weight, mode="fan_out", nonlinearity="relu")
                if m.bias is not None:
                    fan_in, _ = M.init.calculate_fan_in_and_fan_out(m.weight)
                    bound = 1 / math.sqrt(fan_in)
                    M.init.uniform_(m.bias, -bound, bound)
            elif isinstance(m, M.Linear):
                M.init.msra_uniform_(m.weight, a=math.sqrt(5))
                if m.bias is not None:
                    fan_in, _ = M.init.calculate_fan_in_and_fan_out(m.weight)
                    bound = 1 / math.sqrt(fan_in)
                    M.init.uniform_(m.bias, -bound, bound)

    def forward(self, x):
        x = F.max_pool2d(F.relu(self.conv1(x)), 2)
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = F.flatten(x, 1)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

custom_init_lenet = CustomInitLeNet()

我们可以直观地感受到，上面的代码根据 module 的类型对 Conv2d 和 Linear 层进行了区分，采取了不同的初始化策略。 针对参数是 weight 还是 bias, 所执行的初始化策略也有所不同。

究竟什么样的初始化策略是最优的呢？目前不用搞清楚背后的原因，我们只需要明白通过 module 和方式来定义模型，比 funtional 更加灵活高效。

经典 CNN 结构实现

研究和工程人员所需要具备的一个重要能力是将通过实验想法转变为现实进行验证，有了 Module 这样强有力的工具，我们要能够做到将想到的模型结构进行高效的实现。但正所谓巧妇难为无米之炊，想要一下子蹦出一个有意思的模型结构是比较困难的。为了避免工程能力成为自己的短板，目前我们需要积累更多的神经网络模型设计的代码经验，一种有效的方式就是根据已有的经典科研文献中的网络模型结构进行实现，学习更多的代码范式，这样在将来才能够放飞自我的想象力。

接下来我们要趁热打铁，借助对 Module 的基本认知，尝试了解一些经典的 CNN 代码实现。

深层卷积神经网络 AlexNet

LeNet 通过引入卷积运算成功证明了 CNN 模型的有效性，但是其网络结构比较浅，简单的模型在面对复杂任务的时候容易力不从心。

接下来，我们利用 Module 来实现一个比 LeNet 更加深的卷积神经网络模型结构，常被称为 AlexNet:

• 注意输入数据的区别： 原始的 AlexNet 论文将模型使用于 ImageNet 数据集，而我们打算将模型用于 CIFAR10 数据集；

• 由于不同数据集输入的数据形状不一致，我们如果想要使用 AlexNet 在 CIFAR10 上进行训练，则需要做一些适应性的变化；

• 一种思路是我们即将采用的：在 Dataloader 中对输入图片进行 Resize 预处理，比如将原本 \(32 \times 32\) 的图片缩放成 \(224 \times 224\) 的图片；

• 另外一种思路是，我们按照输入为 CIFAR10 数据的形状去修改 AlexNet 各层的参数（感兴趣的话可以自己试一下）；

• 对应地，分类的数量也要从原本 ImageNet 数据集的 \(1000\) 修改为 CIFAR10 数据集的 \(10\) 类。

class AlexNet(M.Module):
    def __init__(self, num_classes: int = 10) -> None:
        super().__init__()
        self.features = M.Sequential(
            M.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
            M.ReLU(),
            M.MaxPool2d(kernel_size=3, stride=2),
            M.Conv2d(64, 192, kernel_size=5, padding=2),
            M.ReLU(),
            M.MaxPool2d(kernel_size=3, stride=2),
            M.Conv2d(192, 384, kernel_size=3, padding=1),
            M.ReLU(),
            M.Conv2d(384, 256, kernel_size=3, padding=1),
            M.ReLU(),
            M.Conv2d(256, 256, kernel_size=3, padding=1),
            M.ReLU(),
            M.MaxPool2d(kernel_size=3, stride=2),
        )
        self.avgpool = M.AdaptiveAvgPool2d((6, 6))
        self.classifier = M.Sequential(
            M.Dropout(),
            M.Linear(256 * 6 * 6, 4096, 2048),
            M.ReLU(),
            M.Dropout(),
            M.Linear(4096, 4096),
            M.ReLU(),
            M.Linear(4096, num_classes)
        )

    def forward(self, x: megengine.Tensor) -> megengine.Tensor:
        x = self.features(x)
        x = self.avgpool(x)
        x = F.flatten(x, 1)
        x = self.classifier(x)
        return x

AlexNet 模型中还引入了 Dropout 的概念，我们会在下个教程中描述它的作用。

使用重复层级结构的 VGGNet

我们已经将模型结构显式地分为了特征提取部分 feature 和线性分类 classifier 部分。但有的时候我们会遇到这样一种情况：

• 除了超参数的多次调整与尝试之外，我还想要微调特征提取的逻辑，比如仅改变 Conv2d->ReLU->MaxPool2d 子结构重复的次数；

• 问题在于，这些模块的 channel 参数在不同的层之间会发生变化，因此不能直接进行封装；

• 我们不希望每次都要重新定义整个模型的代码，最好能够有一种技巧对相似的子模块进行重复的利用。

在 VGGNet 中，通过使用循环和子程序，实现了对结构的高效重复，值得我们学习和参考：

class VGG(M.Module):

    def __init__(
        self,
        features: M.Module,
        num_classes: int = 10
    ) -> None:
        super().__init__()
        self.features = features  # 注意这里的 features 将用到下面的一个结构
        self.avgpool = M.AdaptiveAvgPool2d((7, 7))
        self.classifier = M.Sequential(
            M.Linear(512 * 7 * 7, 4096),
            M.ReLU(),
            M.Dropout(),
            M.Linear(4096, 4096),
            M.ReLU(),
            M.Dropout(),
            M.Linear(4096, num_classes),
        )

    def forward(self, x: megengine.Tensor) -> megengine.Tensor:
        x = self.features(x)
        x = self.avgpool(x)
        x = F.flatten(x, 1)
        x = self.classifier(x)
        return x

在上面的代码中实现了最基本的 VGG 类（为了简洁表示，我们省去了参数初始化的代码）。

请欣赏下面一段代码，尝试看出其作用：

from typing import Union, List, Dict, Any, cast

def make_layers(cfg: List[Union[str, int]], batch_norm: bool = False) -> M.Sequential:
    layers: List[M.Module] = []
    in_channels = 3
    for v in cfg:
        if v == 'M':
            layers += [M.MaxPool2d(kernel_size=2, stride=2)]
        else:
            v = cast(int, v)
            conv2d = M.Conv2d(in_channels, v, kernel_size=3, padding=1)
            if batch_norm:
                layers += [conv2d, M.BatchNorm2d(v), M.ReLU()]  # 这里出现了 BatchNorm, 我们在下个教程会进行解释
            else:
                layers += [conv2d, M.ReLU()]
            in_channels = v
    return M.Sequential(*layers)

cfgs: Dict[str, List[Union[str, int]]] = {
    'A': [64, 'M', 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
    'B': [64, 64, 'M', 128, 128, 'M', 256, 256, 'M', 512, 512, 'M', 512, 512, 'M'],
    'D': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 'M', 512, 512, 512, 'M', 512, 512, 512, 'M'],
    'E': [64, 64, 'M', 128, 128, 'M', 256, 256, 256, 256, 'M', 512, 512, 512, 512, 'M', 512, 512, 512, 512, 'M'],
}

• 可以发现在 make_layers 中产生的序列会是 Conv2d(->BatchNorm2d)->ReLU->MaxPool2d 的重复；

• 它通过变量 v 的在 cfg 中的循环来将当前的 out_channels 更新为下一步的 in_channels.

这样我们能够很方便地得到层数不同但结构设计相似的 VGG 模型：

def _vgg(cfg: str, batch_norm: bool, **kwargs: Any) -> VGG:
    return VGG(make_layers(cfgs[cfg], batch_norm=batch_norm), **kwargs)

vgg11 = _vgg('A', False)
vgg13 = _vgg('B', False)
vgg16 = _vgg('D', False)
vgg19 = _vgg('E', False)

vgg11_bn = _vgg('A', True)
vgg13_bn = _vgg('B', True)
vgg16_bn = _vgg('D', True)
vgg19_bn = _vgg('E', True)

你可以尝试把这些不同的 VGG 结构 print 出来看看。

使用重复块状结构的 GoogLeNet

AlexNet 和 VGGNet 都是在基于 LeNet 的背景下，选择对模型层数进行加深，试图取得更好的效果。

现在我们将要介绍由 Google 提出的 GoogLeNet(Inception) 模型结构，看其如何处理多分支的块状结构。

注意：我们不会在这里实现完整的模型，仅仅关注其设计的 Inception Block.

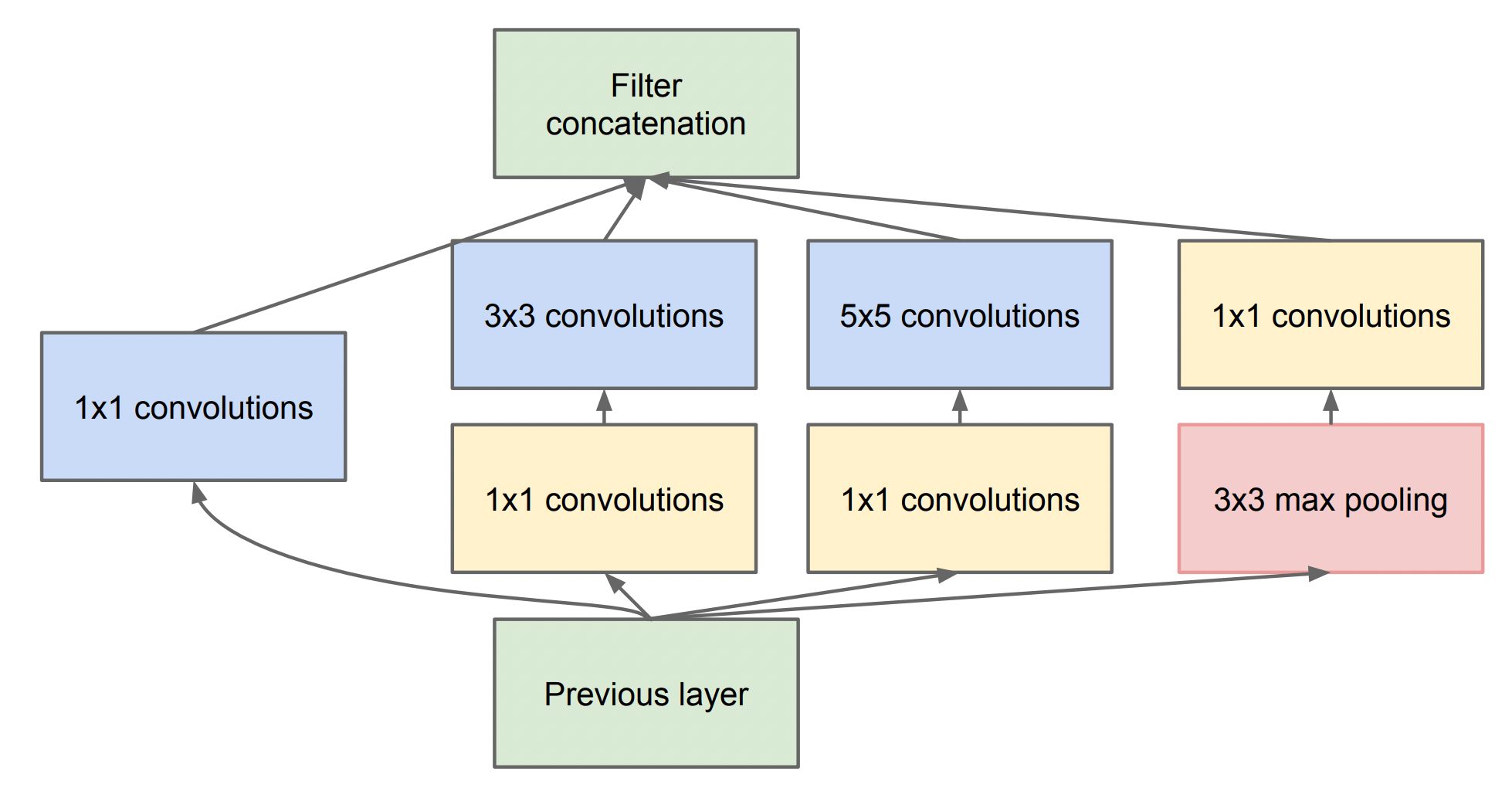
如上图所示（图片来自 原论文），Inception 块由 \(4\) 条分支（Branch）组成：

• 前三条分支使用大小为 \(1 \times 1\) 、\(3 \times 3\) 和 \(5 \times 5\) 的卷积层，负责从不同空间大小中提取信息；

• 中间的两条分支在输入上执行 \(1 \times 1\) 卷积，以减少通道数，从而降低模型的复杂性；

• 第四条分支使用 \(3 \times3\) 最大池化层，然后使用 \(1 \times 1\) 卷积层来改变通道数。

• 最后我们将每条分支的输出在 \(N, C, H, W\) 的 \(C\) 维度上拼接，构成 Inception 块的输出。

与 VGG 的区别在于，在 Inception 块中，通常调整的超参数是每层输出通道的数量。

我们的任务不在于理解当前模型设计的优点，而是要 “看图说话”，实现出 Inception 块结构：

from typing import Optional, Callable

class BasicConv2d(M.Module):

    def __init__(
        self,
        in_channels: int,
        out_channels: int,
        **kwargs: Any
    ) -> None:
        super().__init__()
        self.conv = M.Conv2d(in_channels, out_channels, bias=False, **kwargs)
        self.bn = M.BatchNorm2d(out_channels, eps=0.001)

    def forward(self, x: megengine.Tensor) -> megengine.Tensor:
        x = self.conv(x)
        x = self.bn(x)
        return F.relu(x)

class Inception(M.Module):

    def __init__(
        self,
        in_channels: int,
        ch1x1: int,
        ch3x3red: int,
        ch3x3: int,
        ch5x5red: int,
        ch5x5: int,
        pool_proj: int,
        conv_block: Optional[Callable[..., M.Module]] = None
    ) -> None:
        super().__init__()
        if conv_block is None:
            conv_block = BasicConv2d
        self.branch1 = conv_block(in_channels, ch1x1, kernel_size=1)

        self.branch2 = M.Sequential(
            conv_block(in_channels, ch3x3red, kernel_size=1),
            conv_block(ch3x3red, ch3x3, kernel_size=3, padding=1)
        )

        self.branch3 = M.Sequential(
            conv_block(in_channels, ch5x5red, kernel_size=1),
            conv_block(ch5x5red, ch5x5, kernel_size=3, padding=1)
        )

        self.branch4 = M.Sequential(
            M.MaxPool2d(kernel_size=3, stride=1, padding=1, ceil_mode=True),
            conv_block(in_channels, pool_proj, kernel_size=1)
        )

    def _forward(self, x: megengine.Tensor) -> List[megengine.Tensor]:
        branch1 = self.branch1(x)
        branch2 = self.branch2(x)
        branch3 = self.branch3(x)
        branch4 = self.branch4(x)

        outputs = [branch1, branch2, branch3, branch4]
        return outputs

    def forward(self, x: megengine.Tensor) -> megengine.Tensor:
        outputs = self._forward(x)
        return F.concat(outputs, 1)

在完整的 GoogLeNet 中多次使用了 Inception 块来作为整体模型结构的一部分，这种将采用多分支以及重复结构抽象为块（Block）的思路值得我们借鉴。

深度学习代码的组织形式

通常在一份工程化的代码中，我们会以带参数的命令行的形式来运行 .py 脚本。

例如你在阅读 MegEngine 官方提供的 Models 模型库代码时，可能会看到这样的目录结构：

examplenet/
    README.md
    __init__.py
    config.py
    data.py
    model.py
    train.py
    test.py
    inference.py

顾名思义，不同的 .py 脚本文件负责机器学习流水线中不同的环节（必要的情况下它们会变成单独的子包）：

• README: 说明文件，告诉用户如何使用里面的代码；

• config: 里面通常会存放一些配置加载脚本，以及各种推荐配置文件；

• data: 数据集的获取和预处理，最终满足传入模型的格式；

• model: 定义你的模型结构；

• train: 模型的训练代码，用于训练数据集；

• test: 模型的测试代码，用于测试数据集；

• inference: 模型的推理代码，用于实际数据，比如你自己的一张图片。

一个比较好的例子是 MegEngine/Models 中官方实现的 ResNet.

当然了，不是所有基于深度学习框架的库都组织成这种形式，关键是当你见到它们的时候，要能快速反应过来不同的模块负责做什么样的事情。

args 配置项

在调试模型的过程中，我们需要频繁地改变超参数的值以尝试得到最优的配置，甚至会用原始的表格来记录不同的配置组合所取得的效果。

• 而到目前为止，为了便于交互式学习，我们都是通过 Jupyter Notebook 的形式（.ipynb 格式文件）来交互式地修改每个单元格中的代码；

• 重新运行某个单元格，可以使得新的配置生效；重新跑整个代码也行——但这并不是实际的工程项目中我们会采取的做法。

• 如果你点开了 ResNet 模型的 train.py 源代码，就会发现我们会借助 argparse 模块，使用命令行的形式将参数传入程序中。

在本次教程中，我们可以假设通过命令行传递的参数跑到了 args 对象中，看其如何发挥作用。

# 通常会有默认值，但在此处我们没有设置
class ConfigArgs:
    data_path = None
    bs = None
    lr = None
    epochs = None

# 假定我们是通过命令行传入的参数
# python3 train.py --data_path=“/data/datasets/CIFAR10/” \ ...

args = ConfigArgs()
args.data_path = "/data/datasets/CIFAR10/" # 如果使用 MegStudio, 请设置成 "/home/megstudio/dataset/CIFAR10/"
args.bs = 64
args.lr = 1e-3
args.epochs = 10

用一个简单的例子进行说明，我们在获取数据集的时候，就可以利用到 args.datapath, args.train_bs, args.test_bs 作为参数：

def build_dataset(args):
    transform = T.Compose([
            T.Resize(224),  # 注意：ImageNet 图像大小 224×224, 这也是 AlexNet 和 VGG 的默认输入
            T.ToMode('CHW'),
    ])

    # 处理训练数据集
    train_dataset = data.dataset.CIFAR10(root=args.data_path, train=True, download=False)
    train_sampler = data.SequentialSampler(dataset=train_dataset, batch_size=args.bs)
    train_dataloader = data.DataLoader(
        train_dataset,
        train_sampler,
        transform,
    )

    # 处理测试数据集
    test_dataset = data.dataset.CIFAR10(root=args.data_path, train=False, download=False)
    test_sampler = data.RandomSampler(dataset=test_dataset, batch_size=args.bs)
    test_dataloader = data.DataLoader(
        test_dataset,
        test_sampler,
        transform,
    )

    return train_dataloader, test_dataloader


# 加载训练和测试数据集
train_dataloader, test_dataloader = build_dataset(args)

对一些常见功能进行适当的封装，通过参数进行具体配置的控制，将更有利于进行代码复用。

随着我们阅读过的代码越来越多，我们也会见到更多工程化的代码设计，这些经验将极大提升我们的开发效率。

Module 模型训练和测试

需要注意的是，使用 Module 建模得到的模型 model 可以分为训练和测试两种模式：

• 这是因为一些神经网络算子的行为在不同的模式下也需要不同（尽管我们目前可能还没有用到这些算子）；

• 默认情况下启用训练模式 model.train(), 但在进行模型测试时，需要执行 model.eval() 切换到测试/评估模式。

我们以 AlexNet 为例来测试一下最终的效果：

model = AlexNet(num_classes=10)

import time

def train(model, args):

    gm = autodiff.GradManager().attach(model.parameters())
    optimizer = optim.Adam(model.parameters(), lr=args.lr)

    start_time = time.time()

    for epoch in range(args.epochs):

        running_loss = 0
        nums_train = 0

        for batch_data, batch_label in train_dataloader:
            batch_data = megengine.tensor(batch_data).astype("float32")
            batch_label = megengine.tensor(batch_label)

            with gm:
                pred = model(batch_data)
                loss = F.loss.cross_entropy(pred, batch_label)
                gm.backward(loss)
                optimizer.step().clear_grad()
            running_loss += loss.item()
            nums_train += len(batch_data)

        print("epoch = {}, loss = {:.6f}, time elapsed: {:.2f} min".format(
            epoch+1, running_loss / nums_train, (time.time() - start_time)/60))

train(model, args)

epoch = 1, loss = 0.113663, time elapsed: 0.58 min
epoch = 2, loss = 0.023927, time elapsed: 1.17 min
epoch = 3, loss = 0.021121, time elapsed: 1.75 min
epoch = 4, loss = 0.019437, time elapsed: 2.34 min
epoch = 5, loss = 0.017698, time elapsed: 2.92 min
epoch = 6, loss = 0.016528, time elapsed: 3.51 min
epoch = 7, loss = 0.015457, time elapsed: 4.10 min
epoch = 8, loss = 0.014583, time elapsed: 4.68 min
epoch = 9, loss = 0.013986, time elapsed: 5.26 min
epoch = 10, loss = 0.013647, time elapsed: 5.85 min

注意到以下细节：

• 相较于简单的 LeNet 模型，我们训练更复杂的模型时，单个 epoch 的时间显著地增加了；

• 在第一个 epoch 的训练后，loss 已经比 LeNet 模型训练 10 个 eopch 要低；

• 与此同时，我们训练 10 个 epoch 就已经超过了 LeNet 训练 100 个 epoch 的效果；

• 如果使用更多的时间来训练，loss 值还能继续降低，但是我们也要避免产生过拟合现象。

实际上细心的话你会发现，我们这里使用了 Adam 优化器来代替 SGD, 以使得模型能够更快地收敛。为什么呢？

我们在这个教程中留下了诸多疑点，这些都是关于模型训练方面的经验和技巧，我们会在下一个教程中统一进行解释。

现在我们来测试下模型预测的效果：

def test(model):

    model.eval()
    nums_correct = 0
    nums_test = 0

    for batch_data, batch_label in test_dataloader:
        batch_data = megengine.tensor(batch_data).astype("float32")
        batch_label = megengine.tensor(batch_label)
        logits = model(batch_data)
        pred = F.argmax(logits, axis=1)
        nums_correct += (pred == batch_label).sum().item()
        nums_test += len(batch_data)
    print("Accuracy = {:.3f}".format(nums_correct / nums_test))

test(model)

Accuracy = 0.602

我们在这里仅对不同模型的效果进行了简单的对比，实际上这样的对照不够严谨（没有严格地控制变量），仅仅是为了让你感受复杂模型的有效性。

你可以再多多调教我们的 AlexNet 模型，看能否达到更高的精度。

• 我们经常会在科研文献中看到一个模型在某个 Benchmark 上所取得的最优效果，前沿论文的实验结果通常能达到当前最优（State-of-the-art, SOTA），也容易被后来居上；

• 这通常研究人员需要花费很多的时间和精力去选取合适的超参数，或者对模型结构进行精细的设计和调整，找到最好效果的模型作为实验结果，“刷点”行为在深度学习领域十分常见；

• 但我们在分享自己实验结果的同时，也需要讲究实验的可复现性（Reproducibility），如果一篇深度学习领域论文的实验结果无法被他人复现，则其真实性容易受到质疑。

有了不错的模型，是不是已经开始有分享给别人使用的冲动了呢？接下来我们就将学习如何保存和加载模型。

模型保存与加载

到目前为止，我们一直在关注如何实现并且训练好一个模型。但我们有时需要把训练好的（模型）参数以文件的形式存储在硬盘上，以供后续使用，比如：

• 你预计需要训练超过 1000 个 epoch 的模型，但时间不足，你希望能够将途中模型参数临时保存起来，下次有时间再继续基于保存的参数进行训练；

• 你有充足的时间，但是训练太久容易导致过拟合，因此需要每训练一段时间就保存好当前的模型，根据最终的测试效果选出最优的模型；

• 你需要将训练的模型部署到其它的设备上进行使用（这是另外的使用情景，我们在当前系列的教程中不会接触到）…

最简单的办法是，使用 MegEngine 中提供的 save 和 load 接口，我们以最简单的 Tensor 进行举例：

x = megengine.Tensor([1, 2, 3, 4])

megengine.save(x, 'tensor.mge')
new_x = megengine.load('tensor.mge')

print(new_x)

Tensor([1 2 3 4], dtype=int32, device=xpux:0)

在上面的代码执行过程中 megengine.save() 负责把对象保存成磁盘文件，而 megengine.load() 负责从文件中加载用 save() 所保存的对象。

文件的后缀名其实可以随意选取，比如 .mge, .megengine, .pkl… 等，关键是要让使用的人从后缀名中能判断出加载方式。

我们回顾一下教程开始提到的一个知识点，在每个 Module/Optimizer 对象中，都提供了 state_dict() 方法来获取内部的状态信息：

• Module 的 state_dict() 获取到的是一个有序字典，其键值对是每个网络层和其对应的参数；

• Optimizer 的 state_dict() 获取到的是无序字典，内部有包含优化器参数的 param_groups 和 state 信息。

print(lenet.state_dict().keys())
print(optimizer.state_dict().keys())

odict_keys(['conv1.bias', 'conv1.weight', 'conv2.bias', 'conv2.weight', 'fc1.bias', 'fc1.weight', 'fc2.bias', 'fc2.weight', 'fc3.bias', 'fc3.weight'])
dict_keys(['param_groups', 'state'])

根据我们 save() 和 load() 思路的不同，也导致有好几种不同的处理方式。

保存和加载状态字典

即保存模型的 state_dict(). 这是比较推荐的做法。但是注意：

• 在进行预测之前，必须调用 ``.eval()`` 将一些算子设置成验证状态， 否则会生成前后不一致的预测结果（经常有人忘记这一点）；

• 由于我们保存的是 state_dict(), 在加载时也需要调用模型对应的 load_state_dict() 方法；

• load_state_dict() 方法必须传入一个状态字典，而不是对象的保存路径，也就是说必须先调用 load(), 然后再调用该方法。

megengine.save(model.state_dict(), 'model_param.mge')
new_model = AlexNet()

# ERROR! 这是错误的做法
# new_model.load_state_dict('model_param.mge')

model_state_dict = megengine.load('model_param.mge')  # 反序列化字典对象
new_model.load_state_dict(model_state_dict)

加载后的模型可以继续用于训练或者直接用于预测，这里我们测试一下这个刚加载进来的模型，结果应该与之前保存的模型精度完全一致。

test(new_model)

Accuracy = 0.602

保存和加载整个模型

你也可以选择将整个模型进行保存：

megengine.save(model, 'model.mge')
another_model = megengine.load('model.mge')
test(another_model)

Accuracy = 0.602

这种做法简单粗暴，缺点在于序列化后的数据只适用于特定模型结构，无法做进一步的处理；

使用检查点（Checkpoint）

我们知道了 model 和 optimizer 都能够提供 state_dict 信息，因此一种更加精细的做法是将它们和更多的信息组合起来存储：

megengine.save({
                'epoch': epoch,
                'model_state_dict': model.state_dict(),
                'optimizer_state_dict': optimizer.state_dict(),
                'loss': loss,
                ...
                }, PATH)

这样在加载使用的时候，我们就能够利用更多已经保存下来的信息：

model = TheModelClass(*args, **kwargs)
optimizer = TheOptimizerClass(*args, **kwargs)

checkpoint = megengine.load(PATH)
model.load_state_dict(checkpoint['model_state_dict'])
optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
epoch = checkpoint['epoch']
loss = checkpoint['loss']

将来你会在一些工程化的代码中看到这样的用法，状态信息非常重要，请及时保存，以免丢失。

总结回顾

MegEngine 中的 Module 类为开发者提供了足够程度的抽象，使得我们能够灵活高效地实现各种神经网络的模型结构：

• 我们能够借助 Module.parameters() 方法，快速地获取所有参数的迭代，并且作为 Optimizer 和 GradManager 的输入参数统一管理；

• 通过 Module.init 子模块，模型参数的初始化变得十分简单，我们也能够用自己的逻辑对各层的参数、权重进行更加精细的初始化策略控制；

• 通过 megengine.save() 和 megengine.load() 可以方便地完成状态信息的保存和加载，state_dict 信息可以灵活组合使用。

与此同时，我们也接触到了一些超出深度学习框架服务范围的编程知识，见识到了更多的经典 CNN 结构设计：

• AlexNet: 将卷积神经网络的层数加深，在 CIFAR10 分类任务上取得了更好的效果；

• VGGNet: 利用循环和子程序，可以高效地“配置”出不同类型的 VGG11, VGG13, VGG16, VGG19 模型结构；

• GoogLeNet: 除了不断地加深神经网络的深度，我们也可以像搭积木一样将整个模型看作是由不同的 “块” 组成的大网络。

尽管这些模型主要被用在计算机视觉分类相关的应用上，但其中发展出的设计思想，希望能够给你带来一些启发。

在工程化方面，我们见识到了标准的深度学习工程模型代码长什么样子，这有利于我们将来去阅读其他人复现好的模型代码，或者是将自己的代码组织得更加优雅。

另外我们在举例的过程中提到了 ResNet, 这是再经典不过的 CNN 模型了！当你能够自己实现完整的 ResNet 中 model.py 内部的各种结构时，即意味着你可以从初学者教程“毕业”，以后遇到奇怪的模型结构也能游刃有余。

不过心急吃不了热豆腐，在抵达这个小目标之前，我们还有一段路要走。

问题思考

我们在这个教程中引入了许多新的概念没有解释，比如什么是 Dropout 算子，什么又是 BatchNorm2d 算子？

以及我们一直都没有解释为什么神经网络模型不应该使用零值初始化策略。如果你始终留有疑惑，这是件好事，耐心完成后面的教程，终究会守得云开见月明。

大模型即是正义？

CIFAR10 图片预测的准确率还有很大的提升空间，是不是意味着只要不断加大模型的深度/宽度，让它变得更复杂，加上精细的超参数调整，就总是能够取得更好的效果呢？

你是否思考过这样一个明显的问题：VGG 论文中设计出了 VGG11, VGG13, VGG16, VGG19… 为什么不搞出一个 VGG100 模型呢？直接 VGG6666 岂不是无敌？

• 一个比较直接的原因是，大模型的计算量更大，训练起来的时间成本和经济成本也更高，耗电也多（我们需要有环保意识）；

• 我们在处理机器学习任务时，不但要考虑精度，还要考虑速度——比如与目标检测/追踪有关的应用就很在意推理时的速度；

• 实际上，不使用 VGG6666 模型的背后还有着其他的原因，我们在下个教程中将进行解释。

这个教程中也给你留下了一个挑战，我们没有完整地写出 GoogLeNet 模型，请你试试能否独立地实现出 GoogLeNet, 甚至是整个 Inception Net 系列的网络结构。

知其然，知其所以然

如果你尝试自己训练过上面的几个模型，修改过不同的超参数方案组合，还可能会遇到如下一些情况：

• 我的 Loss 在训练几个 epoch 之后就不下降了，有时甚至从来没有下降过！

• 我的 Loss 从第一个 epoch 开始就显示为 NaN, 发生什么事了？

• 训练一个 epoch 的成本比之前高了很多，寻找合适的超参数会花掉很多时间…

除此以外，在不改变模型结构的情况下，我们还在代码中进行了一些修改，比如我们改变了超参数，对输入数据进行了预处理，模型参数使用了除零值之外其它的初始化策略。这些修改背后的直觉是什么，当我们需要用神经网络解决不同的任务时，有没有什么经验可循？对于这些深度学习炼丹老师傅们再熟悉不过的一些 “玄学” 现象，如果能分析出问题背后可能的原因，一定会很有成就感。

对于深度学习初学者来说，经典论文的复现是一个比较有趣的练习方式，我们在介绍 AlexNet 和 VGGNet 时给出了 Paper with Code 的网站链接，里面是一个巨大的宝库。你可以尝试参照着一些其他人复现过的模型代码，实现自己的 MegEngine 版本，看看是否能达到一样的效果，我们鼓励你以开源的方式将它们分享出来。最有效的实践方式就是：多看，多写，多想。我们在接下来的教程中，将会一起探索一些炼丹玄学现象背后的原因，总结出一些神经网络模型训练中的常见技巧。

深度学习，简单开发。我们鼓励你在实践中不断思考，并启发自己去探索直觉性或理论性的解释。

上一页

构建更好的模型：神经网络

下一页

神经网络训练技巧