构建更好的模型：神经网络¶

在 MegStudio 运行	查看源文件

我们已经对机器学习的基础流程有了一定的印象，并尝试用线性模型分别在 “新手级别” 的房价回归和手写数字分类任务上取得了不错的效果。

打怪升级的道路还在继续，我们的任务依旧是图像分类，但本次教程较之前又确实有所不同：

我们将回收上一个教程埋下的伏笔，了解另一个计算机视觉领域的经典数据集 CIFAR10, 一起看看数据特征的变化会带来什么样的挑战；
我们还将开动脑筋，分析已有局面，尝试去构建更好的模型——
思路一：改变模型的结构，这意味着我们要认知到线性模型在结构上的局限性；
思路二：改变特征提取的方式，此时我们更多地要从数据的角度去思考，看看传统计算机视觉方法带来了什么样的启发；

请先运行下面的代码，检验你的环境中是否已经安装好 MegEngine（安装教程）：

[1]:

import megengine

print(megengine.__version__)

1.5.0

接下来，我们将先了解一下这次要使用到的经典数据集：CIFAR-10 数据集。

CIFAR-10 数据集¶

CIFAR-10 数据集包含共计 10 个类别的 60000 张 32x32 彩色图像，每个类别包含 6000 个图像，对应有 50000 张训练图像和 10000 张测试图像。

同样地，在 MegEngine 的 dataset 模块中内置了 CIFAR-10 数据集的相关接口，方便初学者进行相关调用：

[2]:

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from megengine.data.dataset import CIFAR10

np.random.seed(20200325)

# 强烈推荐使用 MegStudio 平台，可在项目设置中直接选用 CIFAR10 数据集，无需再进行下载
# 如果使用 MegStudio 环境，请将 MNIST_DATA_PATH 为 /home/megstudio/dataset/CIFAR10/
# 国内网络环境从 CIFAR10 数据集官方主页下载数据集可能会有些慢，可人为下载好以下文件后，放置在 CIFAR10_DATA_PATH 对应的路径
CIFAR10_DATA_PATH = "/data/datasets/CIFAR10/"

# 获取训练数据集，如果本地没有数据集，请将 download 参数设置为 True
train_dataset = CIFAR10(root=CIFAR10_DATA_PATH, train=True, download=False)
print(train_dataset.meta)
print(len(train_dataset), type(train_dataset[0]))
print(len(train_dataset[0]), train_dataset[0][0].shape, train_dataset[0][1].shape)

{b'num_cases_per_batch': 10000, b'label_names': [b'airplane', b'automobile', b'bird', b'cat', b'deer', b'dog', b'frog', b'horse', b'ship', b'truck'], b'num_vis': 3072}
50000 <class 'tuple'>
2 (32, 32, 3) ()

以训练集为例，你最终将得到一个长度为 50000 的 train_dataset 列表，其中的每个元素是一个包含样本和标签的元组：

[3]:

print(train_dataset.meta)
print(len(train_dataset), type(train_dataset[0]))
print(len(train_dataset[0]), train_dataset[0][0].shape, train_dataset[0][1].shape)

{b'num_cases_per_batch': 10000, b'label_names': [b'airplane', b'automobile', b'bird', b'cat', b'deer', b'dog', b'frog', b'horse', b'ship', b'truck'], b'num_vis': 3072}
50000 <class 'tuple'>
2 (32, 32, 3) ()

为了方便理解，我们这里选择将数据集拆分为样本和标签，处理成 Numpy 的 ndarray 格式：

[4]:

train_data = np.array([t[0] for t in train_dataset])
train_label = np.array([t[1] for t in train_dataset])
print(train_data.shape, train_label.shape)

(50000, 32, 32, 3) (50000,)

经过上面的整理，我们得到了训练数据 train_data 和对应的标签 train_label:

可以发现此时的训练数据的形状是 \((50000, 32, 32, 3)\), 分别对应数据量（Number）、高度（Height）、宽度（Width）和通道数（Channel），简记为 NHWC；
你应该发现了，MNIST 数据集中的通道数为 1, 均为灰度图；而 CIFAR-10 数据集的通道数为 3, 数据集中的图像是彩色的；通道数和颜色之间有什么关系呢？

理解彩色图像数据¶

我们先尝试对数据进行随机抽样，并进行可视化显示：

[5]:

import cv2   # 我们后面会提到 cvtColor 方法，因此要用到 cv2 库（OpenCV）

classes = ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
samples_per_class = 7

# 注意：初学者在接触本小节的可视化代码时可不求甚解，只在意其展示效果并阅读后面的部分，学有余力者可尝试搞清楚代码细节。
# 注意：这里我们已经使用 cvtColor 对图像进行了处理
for y, cls in enumerate(classes):
    idxs = np.squeeze(np.where(train_label == y))
    idxs = np.random.choice(idxs, samples_per_class, replace=False)
    for i, idx in enumerate(idxs):
        plt_idx = i * num_classes + y + 1
        plt.subplot(samples_per_class, num_classes, plt_idx)
        plt.imshow(cv2.cvtColor(train_data[idx], cv2.COLOR_BGR2RGB))
        plt.axis('off')
        if i == 0:
            plt.title(cls)
plt.show()

../../_images/getting-started_beginner_how-to-build-a-better-model_11_0.png

挑选出一张图片（下方的 idx 可修改），进行可视化：

[6]:

idx = 10086 # 可以修改这个值
plt.title("The label is: %s" % classes[train_label[idx]])
plt.imshow(train_data[idx])
plt.show()

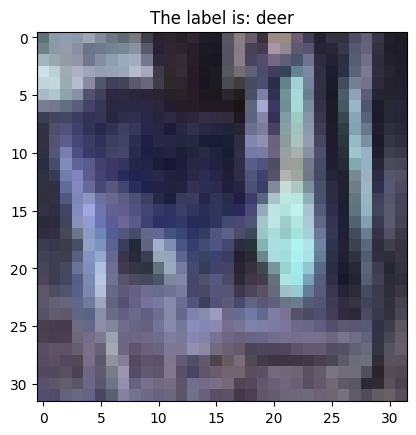
../../_images/getting-started_beginner_how-to-build-a-better-model_13_0.png

你是否会觉得有一些奇怪，为什么这张图片的颜色给人感觉有些奇怪呢？

出于历史原因， OpenCV(cv2) 图像库默认使用 BGR 的颜色通道，而不是一般约定的 RGB 格式。
这就导致当 plt.imgshow() 尝试以 RGB 顺序去读取一张 BGR 格式的图片时，显示的内容会不如预期。
好在 cv2 中也提供了 cvtColor 功能，能够改变图像的通道排序。

如果你使用过老前辈级别的深度学习框架 Caffe, 应该会对此颇有感触。在 MegEngine 的 funtional.vision 模块中也实现了 cvt_color, 区别在于要求输入的数据类型是 Tensor, 毕竟 MegEngine 不是计算机视觉库，funtional 模块中的接口是为 Tensor 操作而设计的。

[7]:

ori_image = train_data[idx]
cvt_image = cv2.cvtColor(ori_image, cv2.COLOR_BGR2RGB)
plt.imshow(cvt_image)
plt.show()

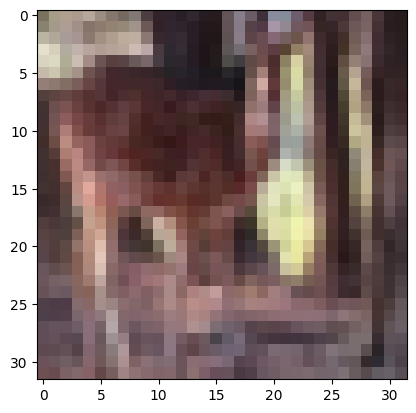
../../_images/getting-started_beginner_how-to-build-a-better-model_15_0.png

我们可以分别对三个颜色通道进行可视化（下面的代码看不懂也没关系，看图）：

[8]:

from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter

split_image = cv2.split(cvt_image)  # 划分为 [R, G, B]
color_maps = ['Reds', 'Greens', 'Blues']

fig = plt.figure(figsize=plt.figaspect(0.5))

for channel_idx, color in enumerate(color_maps):
    ax = fig.add_subplot(2, 3, channel_idx+1, projection='3d')
    ax.set_zlim(-10, 255)
    ax.view_init(elev=45, azim=10)
    X, Y = np.meshgrid(np.arange(32), np.arange(32))
    Z = np.squeeze(split_image[channel_idx])
    surf = ax.plot_surface(Y, X, Z, cmap=color)
    plt.colorbar(surf, shrink=0.5, aspect=8)

    plt.subplot(2, 3, channel_idx+4)
    plt.imshow(split_image[channel_idx], cmap=color)

plt.show()

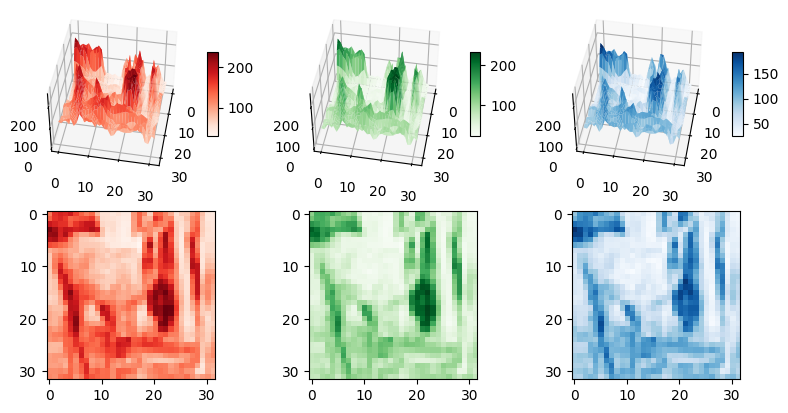
../../_images/getting-started_beginner_how-to-build-a-better-model_17_0.png

数字图像基础和背后的历史知识可有趣啦，一时半会儿也讲不完。在这次的教程中，我们目前只需要明白：

可见光谱中的大部分颜色可以由三种基本色光按不同的比例混合而成，这三种基本色光的颜色就是红、绿、蓝三原色光。
这意味着相较于灰度图，RGB 图中的每个像素都是由 \(3\) 个在 \([0, 256)\) 的值进行颜色组合表示的，对应十六进制范围 #000000 ~ #FFFFFF.

不妨先自己想一想，这样的数据给我们带来了什么样的挑战？线性模型存在着什么样的局限性，我们又该如何去解决它们。

更复杂的计算图结构¶

我们曾提到任何一个神经网络结构都可以用计算图来表示，而在神经网络中应该有非常多的节点（神经元），以下图为例：

上图中的左图可以表示一张 \(4\times 4\) 的单通道图像经过线性分类器输出 10 个值的过程——只有输入和输出两层，似乎和 “深度” 学习没什么关系。

输入层（Input layer）：顾名思义，即我们在一开始输入模型的数据，比如被展平后的灰度图像，每个像素数据点就是输入层的一个神经元；
输出层（Output layer）：对于二分类任务，输出一个概率值，可以用一个神经元来表示；对于多分类任务，则需要用多个神经元表示；
假设我们现在希望有一个更多层的网络结构——
此时需要引入中间层，隐含在输入和输出之间，因此通常也称为隐藏层（Hidden layer）；
在不做任何处理的情况下，每一层的输入都会是上一层线性函数的输出。

但请注意，如果仅仅是简单堆叠神经元之间的全连接层的话，将导致网络最终的输出依旧是输入特征值的线性组合。

仅用语言描述可能有些抽象，我们用代码验证一下：

[9]:

np.random.seed(20200325)
x = np.random.random((4 * 4)) # 随机生成一个 4x4 “图像“，展平成列向量

# 我们假设下面的这些参数都是已经被训练好的，可直接用于预测
W1 = np.random.random((12, 4 * 4))
b1 = np.random.random((12))
W2 = np.random.random((10, 12))
b2 = np.random.random((10))

def two_layer_linear_model(inp):
    z1 = np.dot(W1, inp) + b1
    z2 = np.dot(W2, z1) + b2
    return z2

def one_layer_linear_model(inp):
    w = np.dot(W2, W1)
    b = np.dot(W2, b1) + b2
    z = np.dot(w, inp) + b
    return z

print(two_layer_linear_model(x) - one_layer_linear_model(x) < 1e-7)

[ True  True  True  True  True  True  True  True  True  True]

上面的例子展示了：在假定模型参数已经训练收敛的情况下，单层的线性模型和双层的线性模型有着一样的预测效果（显然，更多层也一样）。

对于双层模型，\(\hat{y} = W2 \cdot (W1 \cdot \mathbf{x} + b1) + b2\), 其中 \(W1, W2, b1, b2\) 是最终学得的参数；
对于单层模型，\(\hat{y} = W \cdot x + b\), 其中 \(W, b\) 是最终学得的参数；
真相是，在理想情况下，我们最终学到的参数将满足 \(W = W2 \cdot W1\), \(b = W2 \cdot b1 + b2\), 因此两个模型预测能力一致。

可见线性层的叠加不但没有带来预测效果上的变化，还额外引入了更多需要被学习和优化的参数，加大了训练过程中的计算量。

非线性激活函数¶

人们期望神经网络可以模拟任意的函数，而线性模型表达能力不够，因此光靠线性计算是不足以解决问题；
受到生物学启发，人脑神经元的树突多呈树状分支，它可接受刺激并将冲动传向胞体；
为了模拟这一机制，人们需要向神经网络模型中引入非线性因素作为“刺激”。

回忆一下，在二分类任务中常常会使用 Sigmoid 函数作为决策函数进行分类，这是我们对它的第一印象。

但仔细想想，Sigmoid 函数将前面的线性计算所得到的输出以 非线性 的形式映射到了 \((0, 1)\) 区间，这个特性可以给我们带来什么启发呢？

[10]:

def sigmoid(x):
    return 1. / (1. + np.exp(-x))

x = np.arange(-10, 10, 0.2)
y = sigmoid(x)
plt.plot(x, y)
plt.show()

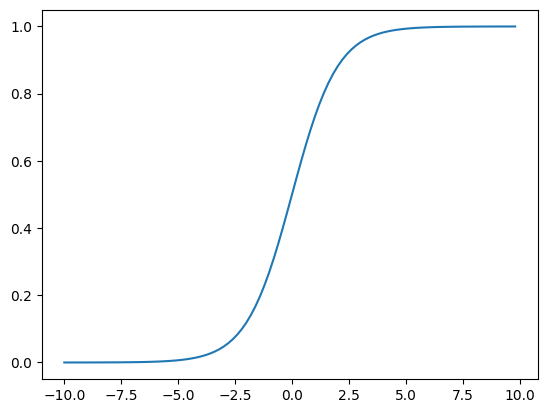
../../_images/getting-started_beginner_how-to-build-a-better-model_23_0.png

这显然让人联想到，Sigmoid 函数非常适合用来当作神经网络中的激活函数，给整个模型引入非线性。

MegEngine 中实现了非常多常见的非线性激活函数，至于究竟选取哪一个激活函数，亦或是设计新的激活函数来使用，没有特别的规定。

将激活函数加在每一层的线性计算之后，这一改动使得神经网络模型理论上可以逼近任意的非线性模型。

前馈神经网络¶

前馈神经网络（Feedforward neural network）是一种最简单的人工神经网络（ANN），完全由全连接层构成。除了输入节点，每个节点都是一个带有非线性激活函数的神经元（或称处理单元），克服了感知器不能对线性不可分数据进行识别的弱点。这里我们需要提到一个术语 “多层感知机”（Multilayer perceptron, 简称 MLP），它的使用有些含糊不清：有的时候被模糊地认为是前馈神经网络的指代；有时严格指代由多层感知器（类似二分类阈值进行激活）所组成的网络。为了避免歧义，我们在本次教程中只使用 “前馈神经网络” 这种说法，但你应该知道 MLP 在具体的上下文中的指代。

我们现在就可以尝试写出一个糙版本的前馈神经网络，在 MNIST 数据集上进行测试：

[11]:

import numpy as np
import megengine as mge
import megengine.functional as F
from megengine.data.dataset import MNIST
from megengine.data import SequentialSampler, RandomSampler, DataLoader
from megengine.autodiff import GradManager
import megengine.optimizer as optim

MNIST_DATA_PATH = "/data/datasets/MNIST/"  # 记得修改这里的路径

# 设置超参数
bs = 64
lr = 0.75
epochs = 5
num_hidden_1 = 256
num_hidden_2 = 128

# 读取原始数据集
train_dataset = MNIST(root=MNIST_DATA_PATH, train=True, download=False)
num_features = train_dataset[0][0].size
num_classes = 10

# 训练数据加载与预处理
train_sampler = SequentialSampler(dataset=train_dataset, batch_size=bs)
train_dataloader = DataLoader(dataset=train_dataset, sampler=train_sampler)

# 初始化参数，没有使用零初始化，而是用 NumPy 随机生成服从正态分布的数据，而且加入了缩放因子 Scale
W1 = mge.Parameter(np.random.normal(size=(num_features, num_hidden_1), scale=0.01))
b1 = mge.Parameter(np.random.normal(size=(num_hidden_1,), scale=0.01))
W2 = mge.Parameter(np.random.normal(size=(num_hidden_1, num_hidden_2), scale=0.01))
b2 = mge.Parameter(np.random.normal(size=(num_hidden_2,), scale=0.01))
W3 = mge.Parameter(np.random.normal(size=(num_hidden_2, num_classes), scale=0.01))
b3 = mge.Parameter(np.random.normal(size=(num_classes,), scale=0.01))

# 定义模型
def feedforward_neural_network(X):
    z1 = F.relu(F.matmul(X, W1) + b1)
    z2 = F.relu(F.matmul(z1, W2) + b2)
    z3 = F.matmul(z2, W3) + b3
    return z3

# 定义求导器和优化器
gm = GradManager().attach([W1, b1, W2, b2, W3, b3])
optimizer = optim.SGD([W1, b1, W2, b2, W3, b3], lr=lr)

# 模型训练
for epoch in range(epochs):
    total_loss = 0
    for batch_data, batch_label in train_dataloader:
        batch_data = F.flatten(mge.tensor(batch_data/255), 1).astype("float32")  # 注意这里进行了归一化
        batch_label = mge.tensor(batch_label)
        with gm:
            pred = feedforward_neural_network(batch_data)
            loss = F.loss.cross_entropy(pred, batch_label)
            gm.backward(loss)
            optimizer.step().clear_grad()
        total_loss +=  loss.item()
    print("epoch = {}, loss = {:.6f}".format(epoch, total_loss / len(train_dataset)))

05 10:43:46 process the raw files of train set...
100%|██████████████████████████████████| 60000/60000 [00:01<00:00, 31997.33it/s]
100%|████████████████████████████████| 60000/60000 [00:00<00:00, 1592491.46it/s]

epoch = 0, loss = 0.007613
epoch = 1, loss = 0.002053
epoch = 2, loss = 0.001343
epoch = 3, loss = 0.001037
epoch = 4, loss = 0.000839

[12]:

test_dataset = MNIST(root=MNIST_DATA_PATH, train=False, download=False)
test_sampler = RandomSampler(dataset=test_dataset, batch_size=100)
test_dataloader = DataLoader(dataset=test_dataset, sampler=test_sampler)

nums_correct = 0
for batch_data, batch_label in test_dataloader:
    batch_data = F.flatten(mge.tensor(batch_data/255), 1).astype("float32")   # 注意这里进行了归一化
    batch_label = mge.tensor(batch_label)
    logits = feedforward_neural_network(batch_data)
    pred = F.argmax(logits, axis=1)
    nums_correct += (pred == batch_label).sum().item()
print("Accuracy = {:.3f}".format(nums_correct / len(test_dataset)))

05 10:44:04 process the raw files of test set...
100%|██████████████████████████████████| 10000/10000 [00:00<00:00, 30187.92it/s]
100%|████████████████████████████████| 10000/10000 [00:00<00:00, 1507441.06it/s]

Accuracy = 0.968

我们欣喜地发现，经过 5 个周期的学习，我们的预测精度已经超过了单层的线性分类模型。

你可能已经注意到了一些细节（有一些相当关键！）：

使用全连接层时，每层的参数量是非常大的，这会导致很大的计算和时间开销；
隐藏层神经元个数也是需要人为设计的超参数，并且直接影响到整个网络模型的参数总量；
我们的参数初始化选择了随机初始化而不是零初始化策略， 这是为什么呢？（你可以改回零初始化试试看）
我们还对输入的数据进行了归一化处理，原始值位于 \((0, 255)\), 归一化后统一到 \((0,1)\);
我们选用的激活函数似乎并不是 Sigmoid, 而是一个叫做 ReLU 的家伙。

请尝试修改各种超参数或网络的隐藏层数，看看会得到什么不同的结果。

请停下来看看这个¶

有了前面的理论和实践积累，现在是时候对神经网络的基本结构有更加直观而清晰的认知了。

我强烈推荐你看一看这个系列的视频作为阶段性的总结，绝对会受益匪浅：

3Blue1Brown 深度学习之神经网络的结构 (对于当前教程而言，这个视频是必须观看的)
3Blue1Brown 深度学习之梯度下降法
3Blue1Brown 深度学习之直观理解反向传播
3Blue1Brown 深度学习之反向传播的微积分原理

完整看完第一个视频后，你应该能回答 “为什么要用 ReLU 代替 Sigmoid 作为激活函数” 这个问题了。

而当你将所有的视频看完，你也能更加深刻地体会到 Optimizer 和 GradManager 的魅力～

更巧妙的计算图算子¶

我们在上一小节没有测试前馈神经网络在 CIFAR10 数据集上的效果，你可以自己修改代码测试一下，但预测精度恐怕仍不容乐观。究竟是哪个环节出问题了呢？

回顾一下计算图的基本结构，其中有数据节点（数据和参数）和计算节点（算子）；
前馈神经网络的隐藏层设计可看作是对图结构的宏观调整，而参数的初始化策略也可以被人为控制；
全连接神经网络的各个层之间使用的均为线性算子，我们似乎忽略了算子对整个模型预测性能所带来的影响。

从传统领域知识中学习¶

如今深度学习能够在很多领域大放异彩，离不开其与传统领域知识的结合。

在数字图像处理领域（准确来说是数字信号处理领域），存在着一种名为 “卷积” （Convolution）的操作；
以下面的代码为例子，对于左边的原图，我们定义了两个 \(3\times3\) 卷积核（Filter）对原图进行卷积运算；
可以理解成对于原图中的每个像素，都根据卷积核中给定的参数对周围九宫格的像素值进行加权求和，作为更新后的像素值。

[13]:

image = plt.imread("../../_static/images/chai.jpg")
plt.subplot(131)
plt.axis('off')
plt.imshow(image)

filter1 = np.array([[ -1, -2, -1],
                    [  0,  0,  0],
                    [  1,  2,  1]])
filter2 = np.array([[  0, -1,  0],
                    [ -1,  8, -1],
                    [  0, -1,  0]])

res1 = cv2.filter2D(image, -1, filter1) # 此处 -1 表示自动计算深度，对于 RGB 图，卷积核会自动应用到 3 个通道
res2 = cv2.filter2D(image, -1, filter2) # 我们在进行 reshape 操作时经常也会用到 -1 来进行自动计算

plt.subplot(132)
plt.axis('off')
plt.imshow(res1)
plt.subplot(133)
plt.axis('off')
plt.imshow(res2)
plt.show()

../../_images/getting-started_beginner_how-to-build-a-better-model_30_0.png

背后的细节我们暂时不用深究，直观上给人的感觉是：卷积运算能够对原始图像的空间信息加以利用。

我们在处理图像的时候，使用了 Flatten 算子将一张图片中的像素展平成一个特征向量，结果效果不佳。

有了对卷积的基本了解，这自然地启发我们在神经网络模型中定义一种卷积算子，来作为对图像特征的处理方式。

在 MegEngine 中使用卷积计算¶

在 MegEngine 的 funtional.nn 模块中，实现了卷积相关的算子，我们以 funtional.nn.conv2d 为例子：

假设有一张 \(5 \times 5\) 大小的 2D 单通道图像 input_2d, 像素值分别为 \(0\) 到 \(24\);
我们定义了 \(3 \times 3\) 大小的卷积核 filter_2d 并应用在这张原始图像上，得到了输出图像 output_2d ;
从原始图像中值为 \(6\) 至 \(18\) 的像素，对应值都更新为其上下左右像素值之和（即原始值的 4 倍，对应 \(24\) 到 \(72\)）。

[14]:

input_2d = mge.tensor(np.arange(25).reshape(1, 1, 5, 5)).astype("float32")
filter_2d = mge.tensor(np.array([[0, 1, 0],
                                 [1, 0, 1],
                                 [0, 1, 0]]).reshape(1, 1, 3, 3)).astype("float32")
output_2d = F.nn.conv2d(input_2d, filter_2d)

print(input_2d.numpy())
print(output_2d.numpy())

[[[[ 0.  1.  2.  3.  4.]
   [ 5.  6.  7.  8.  9.]
   [10. 11. 12. 13. 14.]
   [15. 16. 17. 18. 19.]
   [20. 21. 22. 23. 24.]]]]
[[[[24. 28. 32.]
   [44. 48. 52.]
   [64. 68. 72.]]]]

相信你又有了新的疑惑——由于图像边缘的像素存在着 “没有邻居” 的情况，导致卷积计算后舍弃了这些原本位于边缘的像素点，直观来看图像的形状似乎 “小了一圈”，这个情况不是我们所希望的。处理办法是，在计算卷积操作时，先给边缘像素周围补上一圈像素（最常见的操作是补值为 0 的像素点），这样在进行卷积计算的时候，就能利用上原图中的所有像素信息了：

[15]:

input_2d = mge.tensor(np.arange(25).reshape(1, 1, 5, 5)).astype("float32")
filter_2d = mge.tensor(np.array([[0, 1, 0],
                                 [1, 0, 1],
                                 [0, 1, 0]]).reshape(1, 1, 3, 3)).astype("float32")
output_2d = F.nn.conv2d(input_2d, filter_2d, padding=1)  # 注意这一行的变化，Padding = 1 意味着以 1 像素为宽度进行补 0

print(input_2d.numpy())
print(output_2d.numpy())

[[[[ 0.  1.  2.  3.  4.]
   [ 5.  6.  7.  8.  9.]
   [10. 11. 12. 13. 14.]
   [15. 16. 17. 18. 19.]
   [20. 21. 22. 23. 24.]]]]
[[[[ 6.  8. 11. 14. 12.]
   [16. 24. 28. 32. 26.]
   [31. 44. 48. 52. 41.]
   [46. 64. 68. 72. 56.]
   [36. 58. 61. 64. 42.]]]]

用到了卷积算子的神经网络又被人们称为 “卷积神经网络”（Convolutional Neural Network, CNN），从结构上看，它也是前馈神经网络的一种。卷积神经网络常用于计算机视觉领域，上面的 padding 操作也是计算机视觉中常见的图像处理手段，常见的一起搭配使用的算子还有 max_pooling, 可以认为是一种降采样策略，从采样区域内选择最大值进行保留，从而改变了整个长宽比：

[16]:

input_2d = mge.tensor(np.arange(16).reshape(1, 1, 4, 4)).astype("float32")
output_2d = F.nn.max_pool2d(input_2d, kernel_size=2)

print(input_2d.numpy())
print(output_2d.numpy())

[[[[ 0.  1.  2.  3.]
   [ 4.  5.  6.  7.]
   [ 8.  9. 10. 11.]
   [12. 13. 14. 15.]]]]
[[[[ 5.  7.]
   [13. 15.]]]]

不过我们的教程目前还不打算涉及到太多关于计算机视觉相关的内容，因此不打算进行更多这方面的解释。我们需要关注的是：

相较于简单粗暴的 flatten 操作， conv 操作更能够利用图像的空间局部信息；
卷积核中的参数其实和全连接层中的参数类似，都是 “可学习的” ，这意味着我们可以使用深度学习框架来优化卷积神经网络模型；
但请注意：与卷积有关的算子，需要在计算的过程中需要关注不同层形状的变化，否则容易由于形状对不上导致程序报错。

Functional 卷积神经网络¶

结合前面提到的知识，现在我们将构建一个多层的卷积神经网络模型！

由于 MegEngine 默认 Tensor 的数据排布是 \((N,C,H,W)\) 格式，而我们的 CIFAR10 数据集图片是 \((N,H,W,C)\) 格式，所以我们在下面的代码中进行了对应的预处理：

[17]:

import time

import numpy as np
import megengine as mge
import megengine.functional as F
from megengine.data.dataset import CIFAR10
from megengine.data.transform import ToMode, Normalize, Compose
from megengine.data import SequentialSampler, RandomSampler, DataLoader
from megengine.autodiff import GradManager
import megengine.optimizer as optim

CIFAR10_DATA_PATH = "/data/datasets/CIFAR10/"  # 记得修改这里的路径

# 设置超参数
bs = 64
lr = 1e-3
epochs = 100
# 读取原始数据集
train_dataset = CIFAR10(root=CIFAR10_DATA_PATH, train=True, download=False)

# 训练数据加载与预处理
transform = ToMode('CHW')  # (H, W, C) to (C, H, W)
train_sampler = SequentialSampler(dataset=train_dataset, batch_size=bs)
train_dataloader = DataLoader(train_dataset, train_sampler, transform)

# 初始化参数
conv1_weight = mge.Parameter(np.random.normal(size=(6, 3, 5, 5), scale=0.01))
conv1_bias = mge.Parameter(np.random.normal(size=(1, 6, 1, 1), scale=0.01))
conv2_weight = mge.Parameter(np.random.normal(size=(16, 6, 5, 5), scale=0.01))
conv2_bias = mge.Parameter(np.random.normal(size=(1, 16, 1, 1), scale=0.01))
linear1_weight = mge.Parameter(np.random.normal(size=(120, 16 * 5 * 5), scale=0.01))
linear1_bias = mge.Parameter(np.random.normal(size=(120,), scale=0.01))
linear2_weight = mge.Parameter(np.random.normal(size=(84, 120), scale=0.01))
linear2_bias = mge.Parameter(np.random.normal(size=(84,)))
linear3_weight = mge.Parameter(np.random.normal(size=(10, 84), scale=0.01))
linear3_bias = mge.Parameter(np.random.normal(size=(10,), scale=0.01))

param_group = [conv1_weight, conv1_bias,
               conv2_weight, conv2_bias,
               linear1_weight, linear1_bias,
               linear2_weight, linear2_bias,
               linear3_weight, linear3_bias]

# 定义模型
def cnn_model(x):                                          # (3, 32, 32)
    x = F.relu(F.conv2d(x, conv1_weight, conv1_bias))      # (6, 28, 28)
    x = F.max_pool2d(x, 2)                                 # (6, 14, 14)
    x = F.relu(F.conv2d(x, conv2_weight, conv2_bias))      # (16, 10, 10)
    x = F.max_pool2d(x, 2)                                 # (16, 5, 5)
    x = F.flatten(x, 1)                                    # (16 * 5 * 5,)
    x = F.relu(F.linear(x, linear1_weight, linear1_bias))  # (120,)
    x = F.relu(F.linear(x, linear2_weight, linear2_bias))  # (84,)
    x = F.linear(x, linear3_weight, linear3_bias)          # (10,)
    return x

# 定义求导器和优化器
gm = GradManager().attach(param_group)
optimizer = optim.SGD(param_group, lr=lr)

# 模型训练
start_time = time.time()
running_loss = 0
for epoch in range(epochs):

    for batch_data, batch_label in train_dataloader:
        batch_data = mge.tensor(batch_data).astype("float32")
        batch_label = mge.tensor(batch_label)
        with gm:
            pred = cnn_model(batch_data)
            loss = F.loss.cross_entropy(pred, batch_label)
            gm.backward(loss)
            optimizer.step().clear_grad()
        running_loss += loss.item()

    if epoch % 10 == 9:
        print("epoch = {}, loss = {:.6f}, time elapsed: {:.2f} min".format(
            epoch+1, running_loss / (10 * len(train_dataset)), (time.time() - start_time)/60))
        running_loss = 0

epoch = 10, loss = 0.036017, time elapsed: 0.47 min
epoch = 20, loss = 0.036016, time elapsed: 0.94 min
epoch = 30, loss = 0.036015, time elapsed: 1.40 min
epoch = 40, loss = 0.036010, time elapsed: 1.86 min
epoch = 50, loss = 0.031298, time elapsed: 2.33 min
epoch = 60, loss = 0.023354, time elapsed: 2.78 min
epoch = 70, loss = 0.019487, time elapsed: 3.24 min
epoch = 80, loss = 0.016890, time elapsed: 3.69 min
epoch = 90, loss = 0.014909, time elapsed: 4.16 min
epoch = 100, loss = 0.013252, time elapsed: 4.64 min

[18]:

test_dataset = CIFAR10(root=CIFAR10_DATA_PATH, train=False, download=False)
test_sampler = RandomSampler(dataset=test_dataset, batch_size=bs)
test_dataloader = DataLoader(test_dataset, test_sampler, transform)

nums_correct = 0
for batch_data, batch_label in test_dataloader:
    batch_data = mge.tensor(batch_data).astype("float32")
    batch_label = mge.tensor(batch_label)
    logits = cnn_model(batch_data)
    pred = F.argmax(logits, axis=1)
    nums_correct += (pred == batch_label).sum().item()
print("Accuracy = {:.3f}".format(nums_correct / len(test_dataset)))

Accuracy = 0.592

可以看到，经过 100 个周期的训练，这个简陋的模型在 CIFAR10 图片分类上已经能够达到接近 60% 的预测准确率。

实际上，我们这里定义的模型结构是非常经典的 LeNet，只是一些实现细节略有不同；
由于模型变复杂，我们开始计算训练用时，选择每 10 个 epoch 输出一次 Log 信息；
想象一下，如果没有使用 GPU 的话，那将花掉非常多的时间来进行模型训练；
这只是我们对卷积神经网络模型的初体验，我们会慢慢地接触到更多的经典模型！

总结回顾¶

基于线性模型的局限性，我们从不同的角度出发尝试对模型进行了改进，最终取得了不错的效果：

模型结构变得更加复杂，由单层变成多层，为了解决非线性可分问题，我们引入了激活函数这一概念，最终认识了什么是前馈神经网络；
模型算子变得更加精妙，我们借助对传统计算机视觉领域的卷积操作的了解，将隐藏层由简单的全连接层升级成卷积层，卷积神经网络便诞生了。

接下来请在脑中尝试构建出一张完整的计算图，再次回想一下神经网络学习的整个过程：

我们将数据集中的样本经过处理后变为 Tensor 格式，每个样本作为输入层的各个神经节点，开始在图中流动；
在隐藏层中有着许许多多的计算节点，连接着不同节点之间的是需要被学习和优化的参数，也被叫做权重；
前向传播往往会经历特征提取和计算的过程，最终我们会根据任务类型来设计一个损失函数，用来评估训练过程中的模型表现；
反向传播就好像一层层的浪花，根据链式法则去一层一层地计算当前层梯度，然后更新参数，又将梯度信息传给下一层…

问题思考¶

到目前为止，我们一直都在使用 MegEngine 的 functional 模块中的算子来定义我们的模型，一些问题已经初见端倪：

当模型结构开始变得越来越复杂，计算图结构的代码组织工作会变得非常繁杂；
依赖 functional 的定义方式不够灵活，难以精细控制，更难以进行拓展，对业务不友好。

深度学习框架已经为用户简化了梯度的自动求导和参数优化等流程，自然也可以提供一种更加方便的模式来定义我们的模型。

工欲善其事，必先利其器。在下一个教程中，我们将接触到一种更加灵活高效的模型构建方式，这是我们与其它开发者进行沟通的桥梁。

深度学习，简单开发。我们鼓励你在实践中不断思考，并启发自己去探索直觉性或理论性的解释。

从线性回归到线性分类

使用 Module 构造模型结构