点击此处查看上篇文章：（上） 利用 MegEngine 分布式通信算子实现复杂的并行训练

三、简单参数并行

介绍完 MegEngine 的通信算子，我们来了解它们如何使用。首先，让我们从简单参数并行开始，它只涉及 AllGather 这一通信算子。

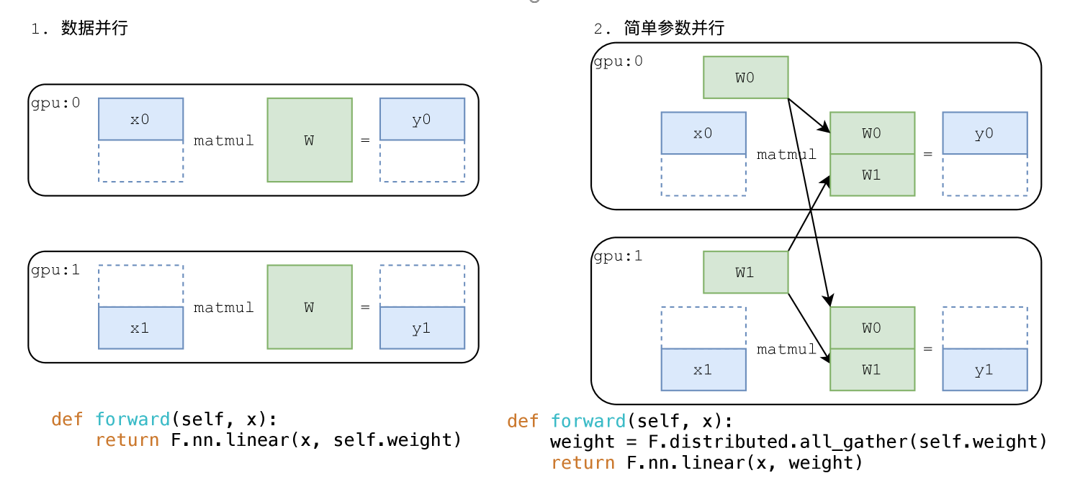
简单参数并行是怎么一回事？我们先用一个简单的全连接层（即矩阵乘法）来回顾一下数据并行——数据并行中，W 是我们的模型（即我们的权重 weight，每张卡拥有一份同样的拷贝），x 是数据。数据并行要求我们将数据平均拆分到每张卡上，2 卡拆 2 份，即 x0 和 x1，4 卡则拆成 4 份，依此类推，各张卡分别进行矩阵乘法计算，得到对应的结果 y。

简单参数并行本质是数据并行的优化？我们不必在每张卡上都放完整的模型，而是只放部分模型，只有在我们需要（即前传）的时候，把分散在各张卡上的参数收集（AllGather）起来参与计算。

如何实现？我们在做矩阵乘法操作之前，先对参数进行 AllGather，从各个节点上收集被我们拆开的参数，AllGather 以后每张卡都有全部的权重了，计算就变得和数据并行一模一样的。所以，简单参数并行的核心操作就是 AllGather，本质用通信来节省显存。

为什么能节省显存呢？我们现在把整个求导过程也画出来了，我们知道在训练一份参数的时候，它其实是会占掉三份显存——参数一份，梯度一份，优化器的 momentum 一份，所以一个参数量 1 million 的模型，如果我们使用数据并行，会占用 3 * 4G = 12G（1 million fp32 类型的数据占用 4G）的显存，那我们一张 2080ti 就完全没有显存可以用于训练了。

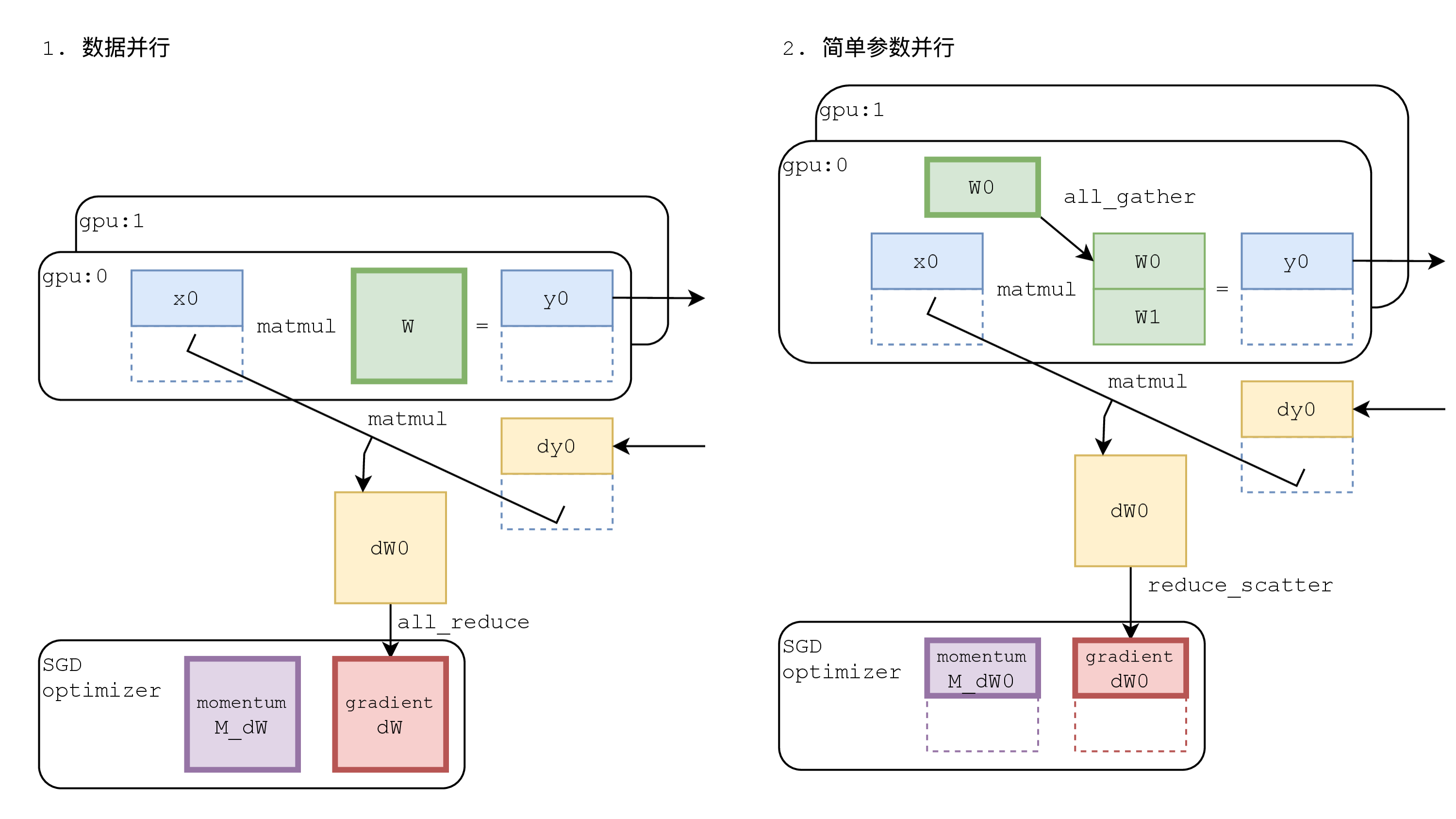
我们再来研究一下这张图，我们在前传的时候做了一次 AllGather，在反传的时候，我们知道 AllGather 的导数是 ReduceScatter，所以，它反传的时候会进行一次 ReduceScatter 。这和数据并行不一样，数据并行前传不需要通信，反传需要进行 AllReduce这是他们的区别。

我们用 MegEngine 写了一套数据并行和简单参数并行的代码，它们有三个不同：

• 一个不同是它们的前传是不一样的——右边（简单参数并行）就是要做一次 AllGather ；
• 还有一个不同就是他们在参数初始化的时候。在数据并行中我们需要参数同步，所以我们要 Broadcast，但是在简单参数并行里面，我们需要的是参数分发，所以用 Scatter，就把它们给分发出去。
• 最后一个不同就是在求导的时候，求导的时候在数据并行当中我们需要进行 AllReduce（MegEngine 使用 AllReduce callback 来支持数据并行），但是在简单参数并行里面不需要进行 AllReduce，自动微分器会负责反传时正确调用 ReduceScatter。

四、层内模型并行

层内模型并行在原理上更加复杂。我们刚才讲的参数并行，它其实是一种层内模型并行的一种特例，因为它非常的简单，只需要对参数进行 AllGather。实际上我们的层内模型并行还有多种不一样的实现。

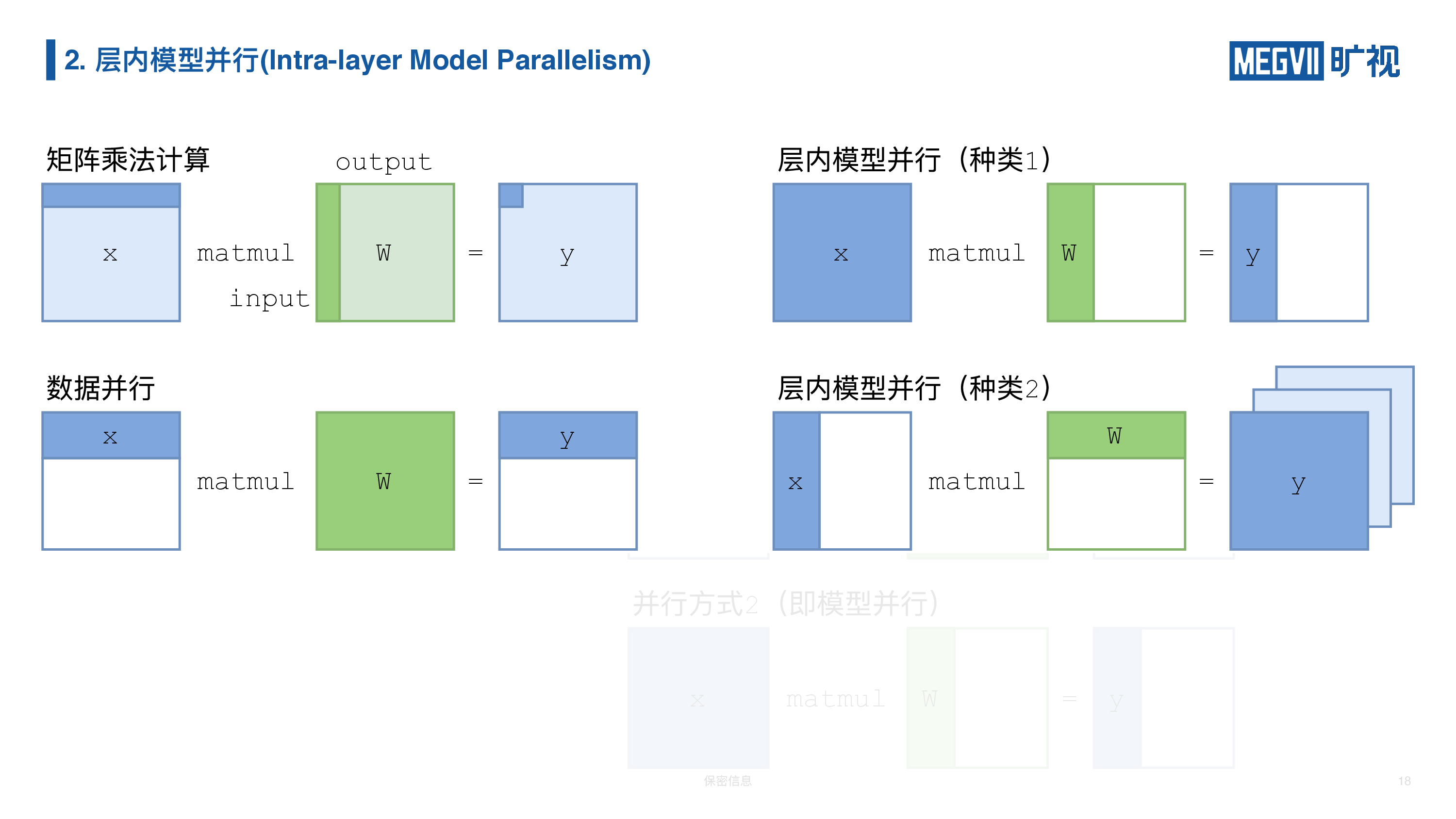
上图给出了完整的矩阵乘法、数据并行和两种模型并行的实现。

我们知道矩阵乘和卷积神经网络中的卷积层（卷积层可以视为对 channel 维度进行的矩阵乘），都天然具有并行的特性。我们在数学意义上的矩阵乘法，每一行每一列的运算都可以独立进行，数据并行就充分的利用了这个特性，我们把数据进行平均切分，各自放在不同的设备上各自做矩阵乘法，最后可以合并起来得到完整结果。

在层内模型并行当中，我们是把每层（全连接/卷积层）的参数矩阵 W 进行切分。一种方式是按输出维度进行切分（纵切）。第二种种类是按输入维度进行切分（横切）。前者在每张卡上得到部分输出维度的对应结果；后者利用了矩阵的低秩特性（Low Rank），每张卡的结果是最终结果的低秩分量，后续须通过 AllReduce 或者 ReduceScatter 将其求和。

接下来我们在多层神经网络中应用层内模型并行——我们实现纯粹的层内模型并行，或者和数据并行搭配使用，完成混合并行。

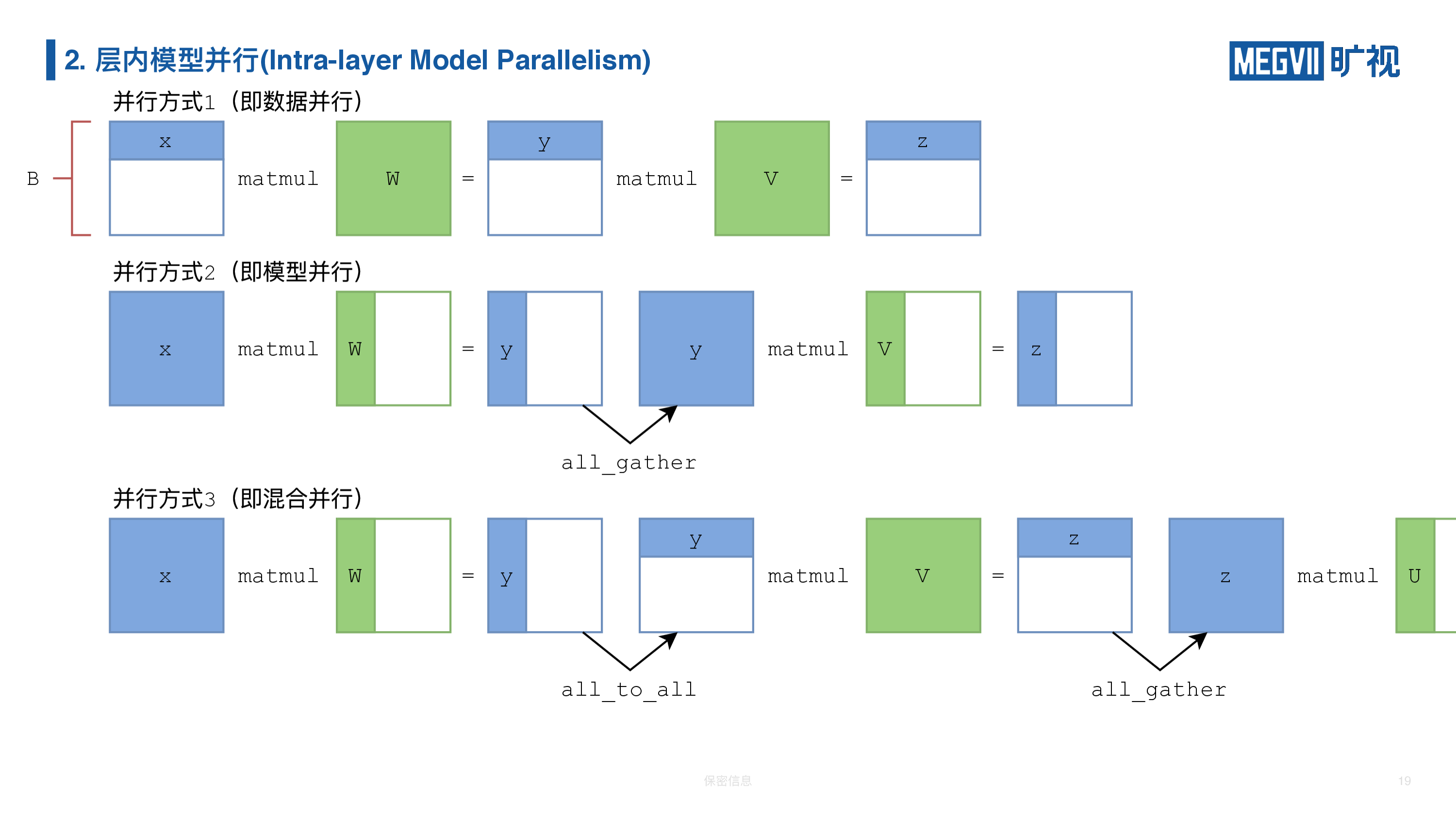
上图第一行是纯数据并行。数据在一开始就被切分到各张卡上，之后不需要进行交换或信息交流，因此数据并行后接数据并行不需要进行特殊操作。

第二种纯层内模型并行。首先你需要完整样本数（batch）的输入特征“X”，最后矩阵乘出来它是完整样本数但部分输出通道数（channel）的特征“Y”，为了后续继续进行模型并行的矩阵乘法，我必须做一次 AllGather，把“Y”沿着通道（channel）收集起来，把它再变成样本数和通道数皆完整的“Y”，再与模型并行的“V”相乘。如果网络继续加深，那么每次矩阵乘结束都要进行 AllGather 操作。

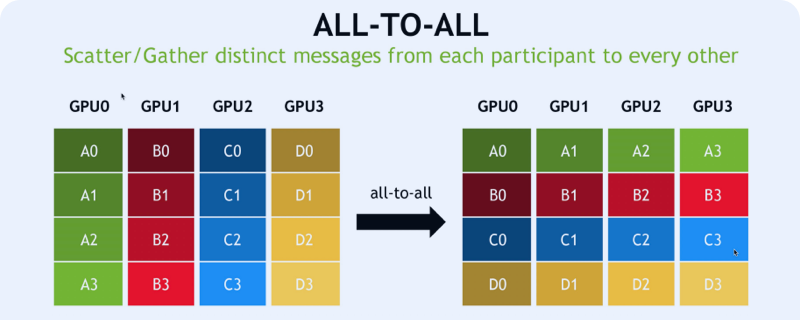
第三种混合并行混合了数据并行与层内模型并行。我们还是以模型并行开始，模型并行的全连接层输出一个纵切的“Y”（即沿输出通道切分的特征 Tensor），但是我们数据并行要的是横切的“Y”（即沿样本数维度切分的特征 Tensor），应该怎么操作？在介绍 MegEngine 通信算子的时候我们提到一个转置操作叫 AllToAll，它可以直接把这个纵切的“Y”变成了横切的“Y”。接下来我们就可以恢复数据并行了，进行一次数据并行的矩阵乘法后，我们还想进行一次模型并行的矩阵乘法，那就再做一次 AllGather，得到全部样本数且全部通道数的完整特征 Tensor。掌握了利用 AllToAll 和 AllGather 实现的“切换”以后，你就可以自己设计与训练混合并行的模型。

接下来我们举例两个应用场景。

场景一：全连接的层内模型并行

我们来进入一个具体场景，在人脸识别任务中应用全连接的层内模型并行。

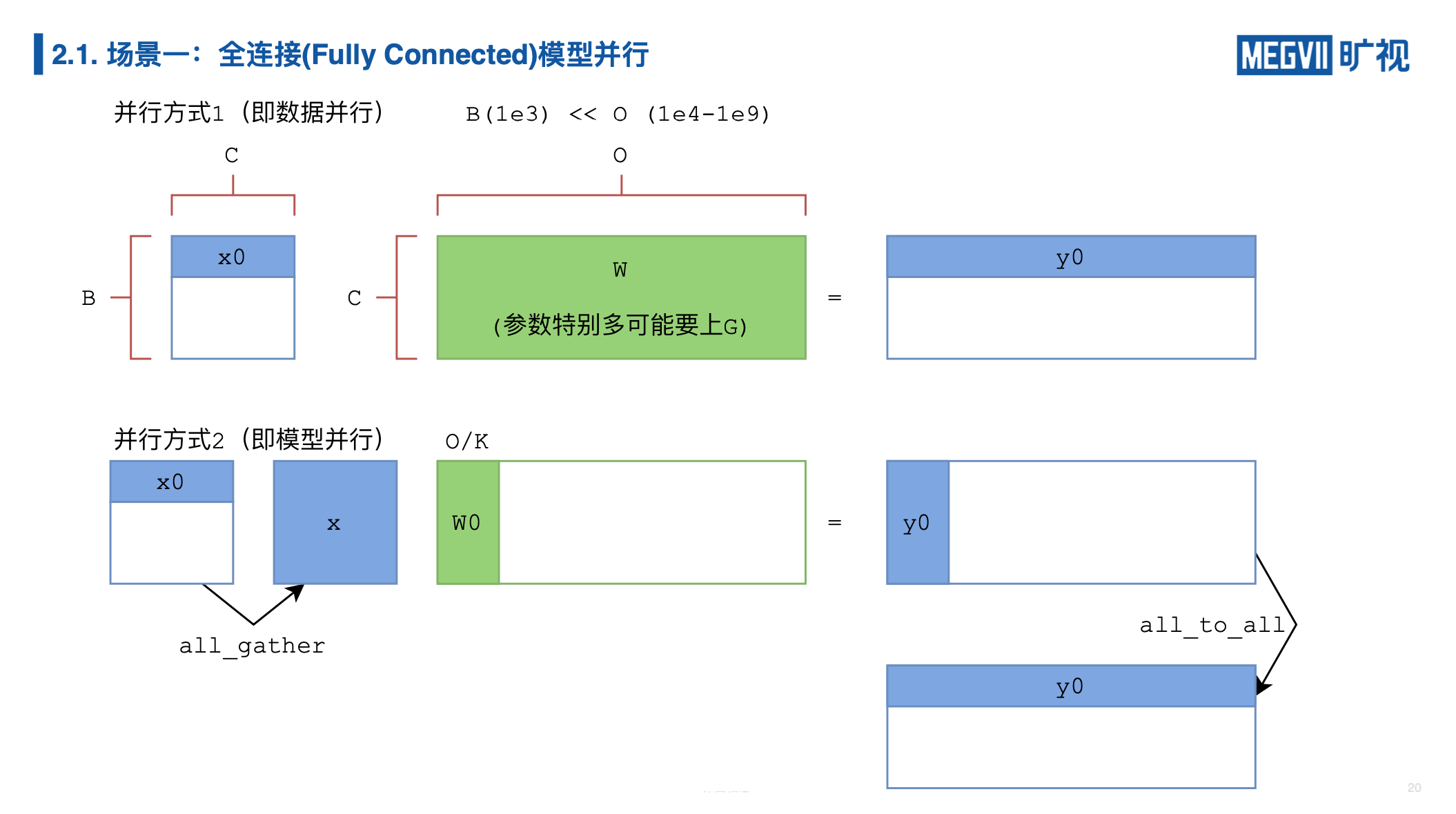
在人脸识别任务当中，可能有百万、千万的 ID（Identity，同一个人为一个 ID），相当于要去做一个输出维度为百万/千万的分类任务，所以，最后这一层，分类的这一层 FC 层（全连接层）它可能参数特别大，比如说我们有一百万（1 million）的 ID，提取的人脸特征是一个 1024 维的向量，它们乘起来就会占用 4 个 G 显存，我们刚才提到 4G 参数的模型在实际训练中会固定占用 3 倍显存，就是 12G，一般的显卡装不下。我只能把这个全连接给放到各张卡上，如果我们有 8 张卡，每张卡就只会分到 1.5G，那么还是可以接受的。这个场景的特点是什么？就是人脸特征维度相比于我的参数矩阵其实非常小的，所以我们对数据进行通信（AllGather），它的代价要比对权重进行通信（AllReduce）它的代价小得多，所以在这个场景下特别适合做模型并行。

在模型并行下分类器 W 输出的结果 Y 的具体含义是什么？我们知道 Y 是竖着切分的，竖着这一维是样本（batch）维，就是它有多少个训练的样本，横着的这一维其实是 ID 维度，就是类别维，表示样本属于各个 ID 的概率，而模型并行下它只输出了一部分标签的概率。求损失函数的时候我们往往用交叉熵（CrossEntropy），交叉熵需要全部的类别概率。没错，利用之前我们介绍的 AllToAll 算子，我们把输出的模型并行的概率矩阵给进行 AllToAll转置，它就变回了数据并行的格式。（讲师注：实际上你并不需要进行 AllToAll，在分类任务的特殊场景下，你并不需要 AllToAll，因为通信代价很大，你可以籍由两次极低代价的通信来实现交叉熵的计算，但是这个超纲了，但不是很困难，留给大家当思考题。）

我们直接上代码。

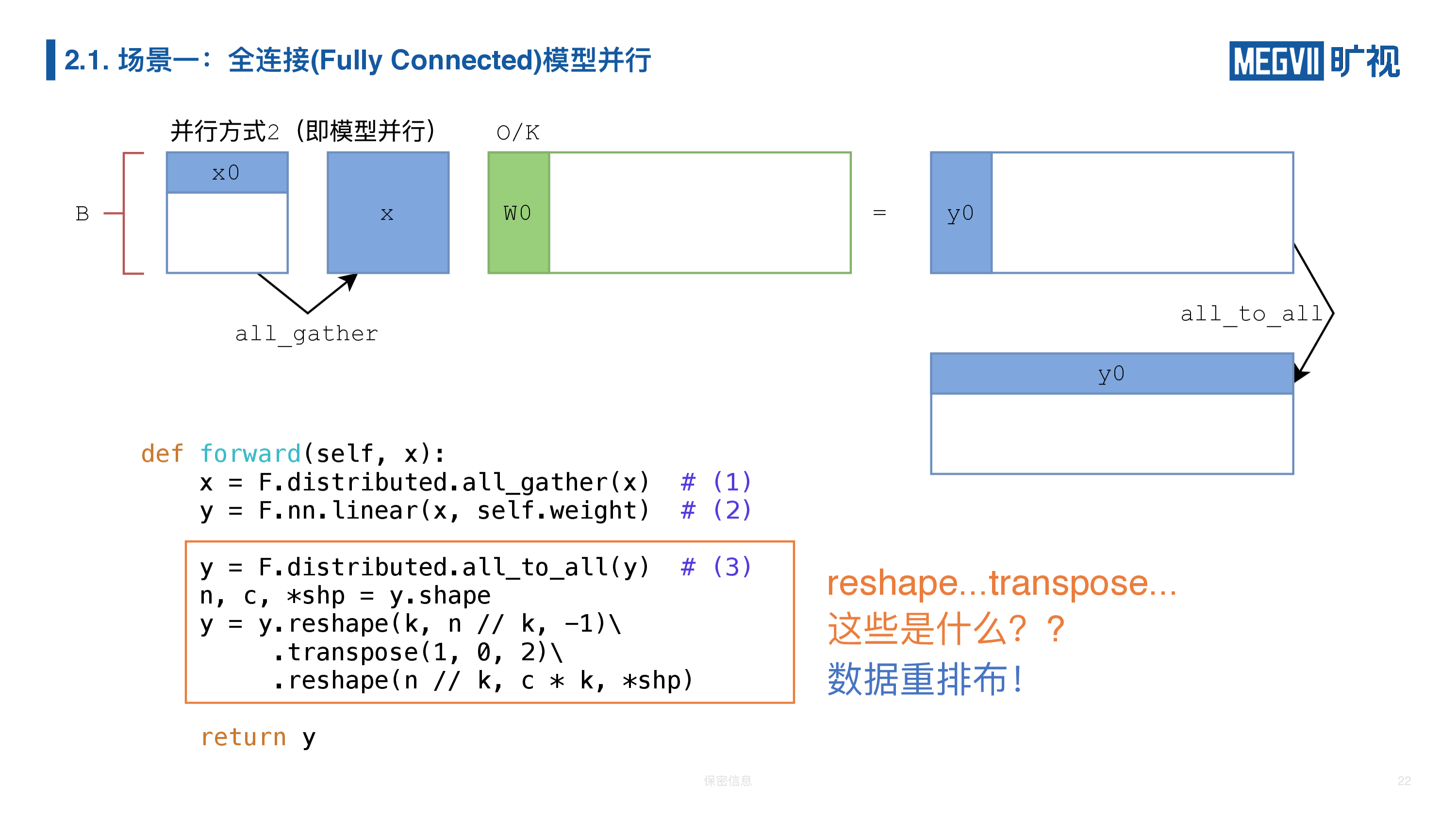
整个过程中有三步，第一步是 AllGather，第二步进行矩阵乘，第三步进行 AllToAll。

那么上图框起来的这段代码是什么东西呢？我们做了这么多 reshape，什么 transpose——这叫数据重排布，我们再花 5 分钟的时间来讲一下数据重排布是什么。

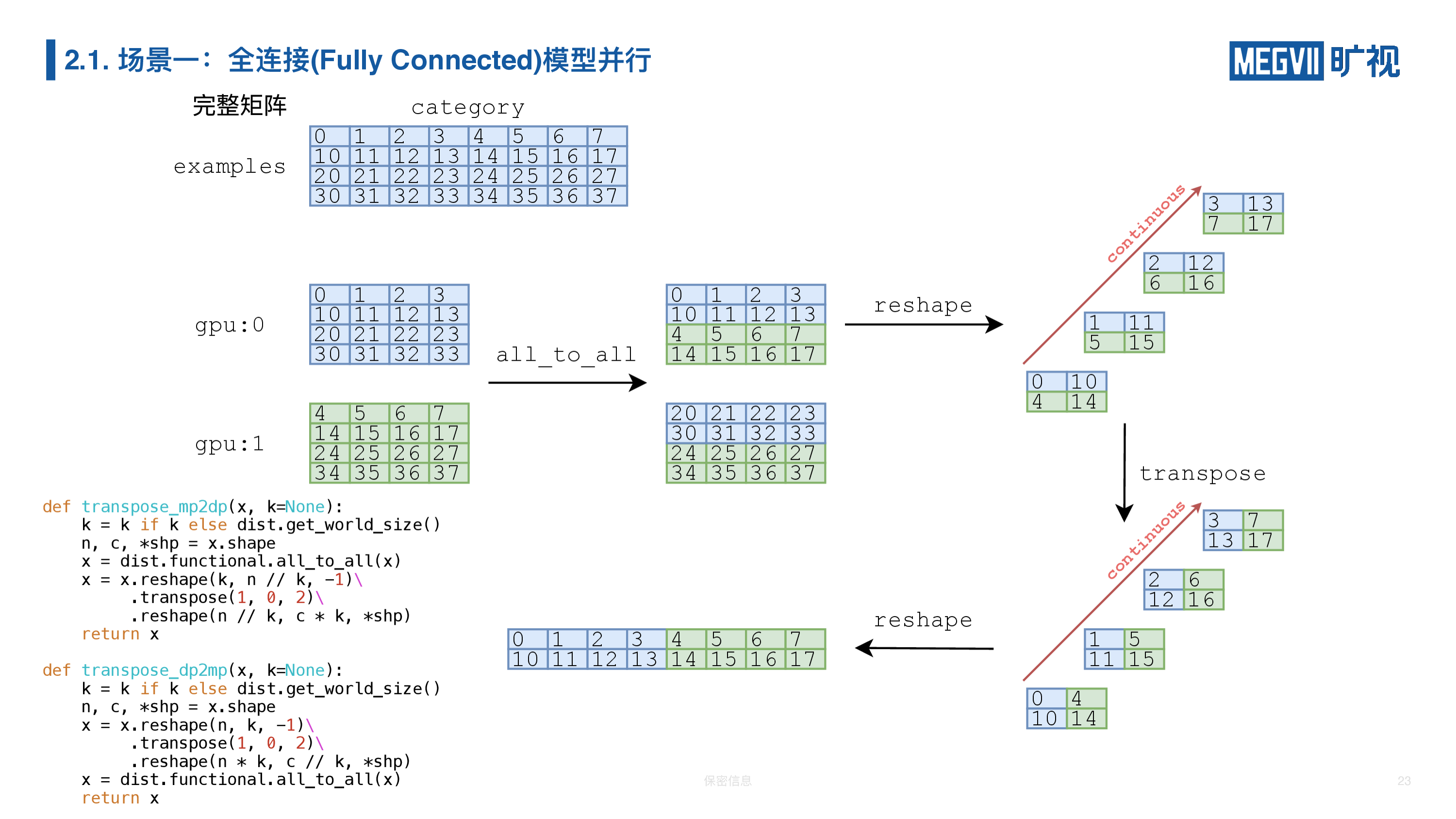
我们 AllToAll 做完以后，得到的其实并不是我们想要的部分数据加上全部分类的一个结果，它其实在底层的数据排布（layout）上面它不是我们期望的。上图是 1 个简化版本的例子，它的分类从 0-7 总共有 8 类，它的样本是 4 张人脸图片。经过模型并行，在卡 0 上面我们得到的输出是 0-3 类的结果，卡 1 上面得到的是 4-7 类的结果。我们做完 AllToAll 以后它变成的矩阵（0,1,2,3,10,11,12,13）并不是我们想要的，我们最后想要的就是 0,1,2,3,4,5,6,7，下面是 10-17，所以的话我们必须先做一次 reshape，沿着这个方向是最里面维 0,1,2,3 数据是连续的，我们把这外面两维（0,10,4,14）个给进行一次转置，就是转过来，最后 reshape 为想要的结果。为了以后使用方便，我简单进行了以下两个封装，上面封装叫 mp2dp，就是从模型并行变成数据并行（Data Parallelism）的一个封装，下面这个是 dp2mp，有了这两个封装以后，我们上面的前传代码就变得简单了。

场景二：组卷积模型并行

讲完了全连接，接下来我们再讲组卷积（Group Convolution），

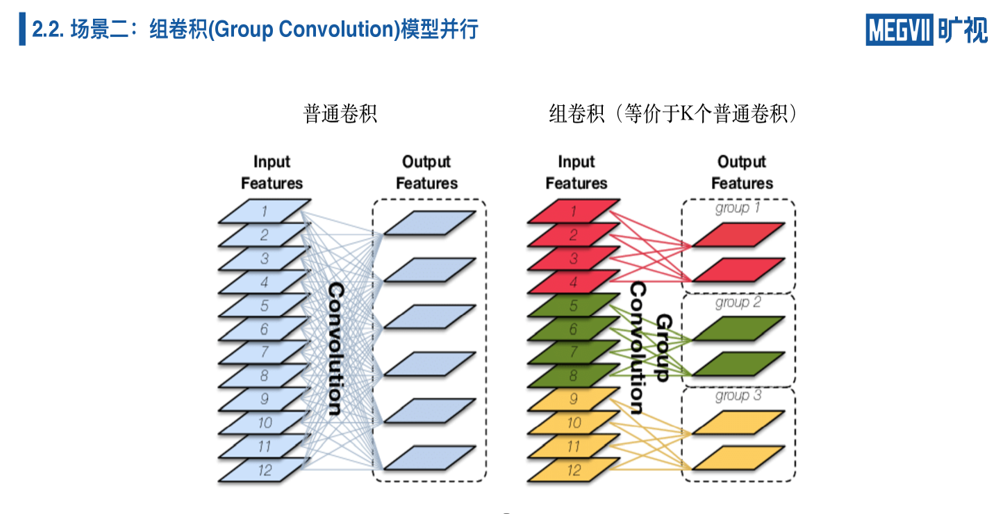
Group Convolution 在我们的移动端模型上面特别常见，组卷积和普通卷积它的区别就在于组卷积相当于 K 个普通卷积。比如说你有三组，就相当于三个普通卷积，但是每个普通卷积都比自己的小，你们也可以发现这个是天然并行的，上图红色的、绿色的、黄色其实可以各自做，在不同的设备上做。

下图用之前二维的表示抽象一下卷积和组卷积的不同——组卷积的模型，它和卷积不一样，组卷积相当于一个稀疏的矩阵乘法，它不是一个稠密的的矩阵（dense matrix）。

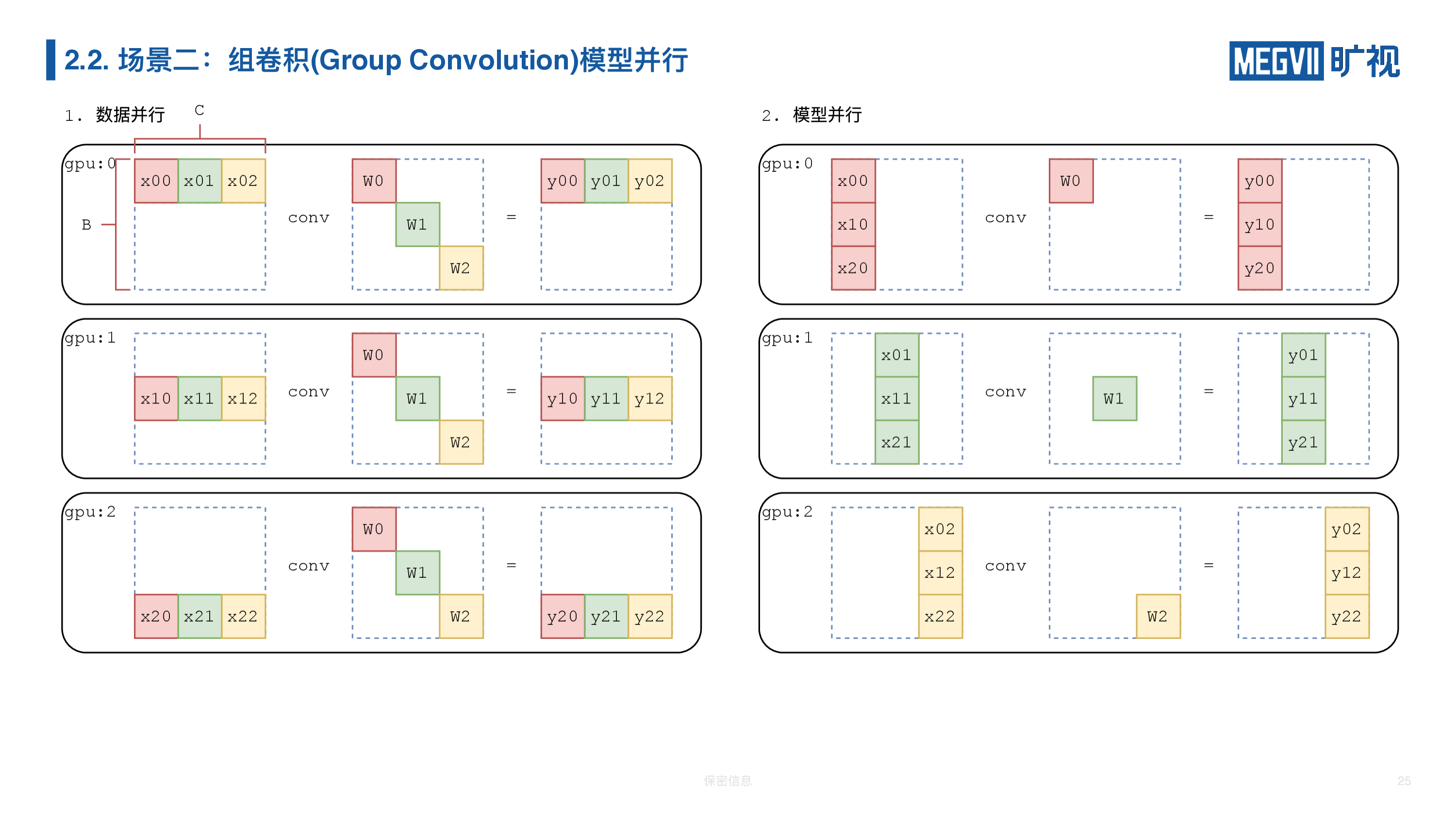
数据并行情况下和普通卷积一样，我们把数据进行切分；模型并行我们可以直接按颜色把这三个组分开，我们第一块卡上做第一个组，第二块卡上做第二个组，第三块卡上做第三个组，对于每块卡来说，原本的组卷积计算都变成了普通的卷积操作。

如果我们前面是普通卷积，中间要插入一组模型并行的组卷积，我们应该怎么样从这两种数据排布之间切换？

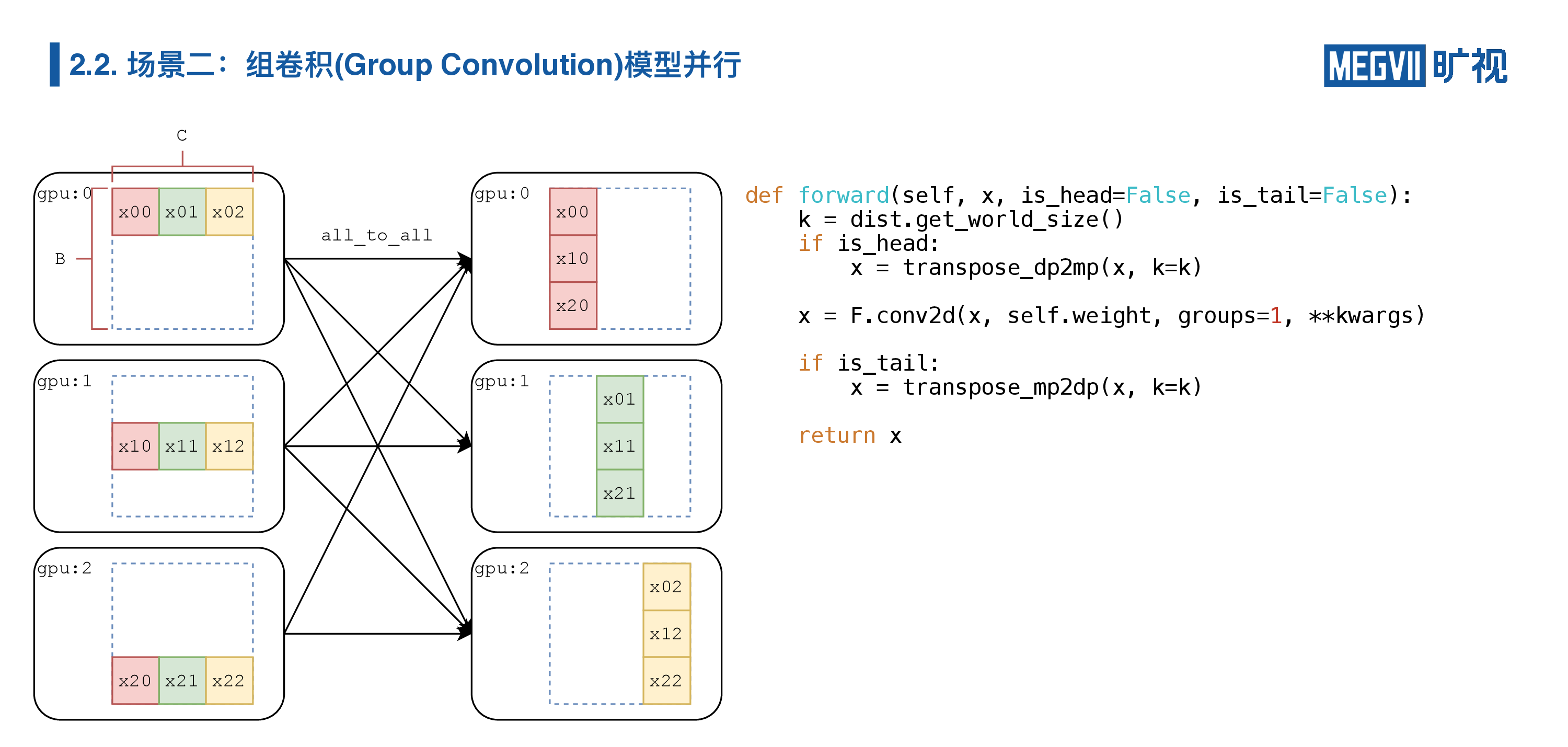
很简单，我们就做一次数据重排布（即 AllToAll），由于是数据并行到模型并行，所以我们调用transpose_dp2mp。

如果我们有多个组卷积，他们连在一起，实际上我们并不需要反复地在数据和模型并行间切换，我们只需要关注头和尾。所以，我们的组卷积在前传函数里面有一个叫 is_head 和 is_tail，我们 is_head 的时候，我们做一次通信， is_tail 的时候再做一次通信，我们中间就完全不需要通信了。

点击此处查看下一篇文章：（下）利用 MegEngine 分布式通信算子实现复杂的并行训练